题目内容
 如图,在△ABC中,BO为边AC上的中线,
如图,在△ABC中,BO为边AC上的中线,| BG |
| GO |
| CD |
| AG |
| AD |
| 1 |
| 5 |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
考点:向量在几何中的应用
专题:计算题,平面向量及应用
分析:先求出
=
(
+
),利用
∥
,设
=k
=
(
+
),可得
=
+
=
•
+(
+1)
,结合
=
+λ
(λ∈R),即可得出结论.
| AG |
| 1 |
| 3 |
| AB |
| AC |
| CD |
| AG |
| CD |
| AG |
| k |
| 3 |
| AB |
| AC |
| AD |
| AC |
| CD |
| k |
| 3 |
| AB |
| k |
| 3 |
| AC |
| AD |
| 1 |
| 5 |
| AB |
| AC |
解答:
解:由已知得G是三角形的重心,因此
=
(
+
),
由于
∥
,因此设
=k
=
(
+
),
那么可得
=
+
=
•
+(
+1)
,
∵
=
+λ
(λ∈R),
∴k=
,∴λ=1+
=
.
故选:B.
| AG |
| 1 |
| 3 |
| AB |
| AC |
由于
| CD |
| AG |
| CD |
| AG |
| k |
| 3 |
| AB |
| AC |
那么可得
| AD |
| AC |
| CD |
| k |
| 3 |
| AB |
| k |
| 3 |
| AC |
∵
| AD |
| 1 |
| 5 |
| AB |
| AC |
∴k=
| 3 |
| 5 |
| 1 |
| 5 |
| 6 |
| 5 |
故选:B.
点评:本题考查向量在几何中的应用,考查平面向量基本定理,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知m∈R,则“m<10”是“lgm<1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
数列{an}满足an=
,则该数列从第5项到第15项的和为( )
|
| A、2016 | B、1528 |
| C、1504 | D、992 |
在△ABC中,角A,B,C的对边分别是a,b,c.已知a=5
,c=10,A=30°,则B等于( )
| 2 |
| A、105° |
| B、60° |
| C、15° |
| D、105° 或 15° |
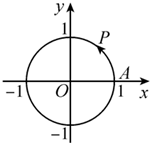 如图,半径为1的圆的圆心位于坐标原点,点P从点A(1,0)出发,依逆时针方向等速沿单位圆周旋转.已知点P在1秒钟内转过的角度为θ(0<θ<π),经过2秒钟到达第三象限,经过14秒钟后又恰好回到出发点A,则θ=
如图,半径为1的圆的圆心位于坐标原点,点P从点A(1,0)出发,依逆时针方向等速沿单位圆周旋转.已知点P在1秒钟内转过的角度为θ(0<θ<π),经过2秒钟到达第三象限,经过14秒钟后又恰好回到出发点A,则θ=