题目内容
已知椭圆
+
=1,(a>b>0)的右焦点为F(c,0),M为椭圆的上顶点,O为坐标原点,且以焦点和短轴的端点为顶点构成边长为
的正方形.
(Ⅰ)求椭圆的方程;
(Ⅱ)是否存在直线l交椭圆于P,Q两点,且使F为△PQM的垂心?若存在,求出直线l的方程;若不存在,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
(Ⅰ)求椭圆的方程;
(Ⅱ)是否存在直线l交椭圆于P,Q两点,且使F为△PQM的垂心?若存在,求出直线l的方程;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出b=1,a=
b=
,由此能求出椭圆方程.
(Ⅱ)假设存在直线l交椭圆于P,Q两点,且使F为△PQM的垂心设P(x1,y1),Q(x2,y2),设直线l的方程为y=x+m,由
,得3x2+4mx+2m2-2=0,由此能求出存在直线l交椭圆于P,Q两点,且使F为△PQM的垂心,直线l的方程为3x-3y-4=0.
| 2 |
| 2 |
(Ⅱ)假设存在直线l交椭圆于P,Q两点,且使F为△PQM的垂心设P(x1,y1),Q(x2,y2),设直线l的方程为y=x+m,由
|
解答:
解:(Ⅰ)∵椭圆
+
=1,(a>b>0)的右焦点为F(c,0),
M为椭圆的上顶点,O为坐标原点,
且以焦点和短轴的端点为顶点构成边长为
的正方形.
∴b=1,a=
b=
,
∴椭圆方程为
+y2=1.…(4分)
(Ⅱ)假设存在直线l交椭圆于P,Q两点,且使F为△PQM的垂心
设P(x1,y1),Q(x2,y2),∵M(0,1),F(1,0),
∴kMF=-1,∴直线l的斜率k=1,∴设直线l的方程为y=x+m,
由
,得3x2+4mx+2m2-2=0,
由题意知△>0,即m2<3,…(7分)
且x1+x2=-
,x1x2=
,
由题意应有
•
=0,又
=(x1,y1-1),
=(x2-1,y2),
∴2x1x2+(x1+x2)(m-1)+m2-m=0…(9分)
2×
-
m(m-1)+m2-m=0,解得m=-
或m=1…(11分)
经检验,当m=1时,△PQM不存在,故舍去m=1,
当m=-
时,所求直线y=x-
满足题意,
综上,存在直线l交椭圆于P,Q两点,且使F为△PQM的垂心,
且直线l的方程为3x-3y-4=0.…(14分)
| x2 |
| a2 |
| y2 |
| b2 |
M为椭圆的上顶点,O为坐标原点,
且以焦点和短轴的端点为顶点构成边长为
| 2 |
∴b=1,a=
| 2 |
| 2 |
∴椭圆方程为
| x2 |
| 2 |
(Ⅱ)假设存在直线l交椭圆于P,Q两点,且使F为△PQM的垂心
设P(x1,y1),Q(x2,y2),∵M(0,1),F(1,0),
∴kMF=-1,∴直线l的斜率k=1,∴设直线l的方程为y=x+m,
由
|
由题意知△>0,即m2<3,…(7分)
且x1+x2=-
| 4m |
| 3 |
| 2m2-2 |
| 3 |
由题意应有
| MP |
| FQ |
| MP |
| FQ |
∴2x1x2+(x1+x2)(m-1)+m2-m=0…(9分)
2×
| 2m2-2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
经检验,当m=1时,△PQM不存在,故舍去m=1,
当m=-
| 4 |
| 3 |
| 4 |
| 3 |
综上,存在直线l交椭圆于P,Q两点,且使F为△PQM的垂心,
且直线l的方程为3x-3y-4=0.…(14分)
点评:本题考查椭圆方程的求法,考查满足条件的直线是否存在的判断与求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若三角形的三条边长分别为3,4,5,则将每条边长增加相同的长度后所得到的新三角形为( )
| A、直角三角形 | B、钝角三角形 |
| C、锐角三角形 | D、不能确定 |
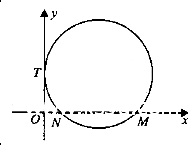 如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3,己知椭圆D:
如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3,己知椭圆D: 如图,△ABC是直角三角形,∠ABC=90°以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.
如图,△ABC是直角三角形,∠ABC=90°以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.