题目内容
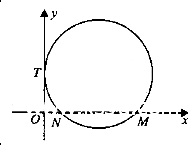 如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3,己知椭圆D:
如图,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M必在点N的右侧),且|MN|=3,己知椭圆D:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(1)求圆C和椭圆D的方程;
(2)若过点M斜率不为零的直线l与椭圆D交于A、B两点,求证:直线NA与直线NB的倾角互补.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件求出圆C的方程为(x-
)2+(y-2)2=
,令y=0,得N(1,0),M(4,0),由
,能求出椭圆D的方程.
(Ⅱ)设直线l的方程为y=k(x-4),由
,得(3+4k2)x2-32k2x+64k2-12=0,设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
,由此能证明直线AN与直线BN的倾斜角互补.
| 5 |
| 2 |
| 25 |
| 4 |
|
(Ⅱ)设直线l的方程为y=k(x-4),由
|
| 32k2 |
| 3+4k2 |
| 64k2-12 |
| 3+4k2 |
解答:
(1)解:设圆半径为r,由题意圆心为(r,2),
∵|MN|=3,∴r2=(
)2+22=
,
∴圆C的方程为(x-
)2+(y-2)2=
,①
在①中,令y=0,得x=1或x=4,∴N(1,0),M(4,0),
由
,得c=1,a=2,b2=4-2=3,
∴椭圆D的方程为
+
=1.
(Ⅱ)证明:设直线l的方程为y=k(x-4),
由
,得(3+4k2)x2-32k2x+64k2-12=0,(*)
设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
,
∵kNA+kNB=
+
=
+
=k
=
[
-
+8]=0,
∴kNA=-kNB.
当x1=1或x2=1时,k=±1,
此时,对方程(*),△=0,不合题意.
∴直线AN与直线BN的倾斜角互补.
∵|MN|=3,∴r2=(
| 3 |
| 2 |
| 25 |
| 4 |
∴圆C的方程为(x-
| 5 |
| 2 |
| 25 |
| 4 |
在①中,令y=0,得x=1或x=4,∴N(1,0),M(4,0),
由
|
∴椭圆D的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)证明:设直线l的方程为y=k(x-4),
由
|
设A(x1,y1),B(x2,y2),则x1+x2=
| 32k2 |
| 3+4k2 |
| 64k2-12 |
| 3+4k2 |
∵kNA+kNB=
| y1 |
| x1-1 |
| y2 |
| x2-1 |
| k(x1-4) |
| x1-1 |
| k(x2-4) |
| x2-1 |
=k
| (x1-4)(x2-1)+(x2-4)(x1-1) |
| (x1-1)(x2-1) |
=
| k |
| (x1-1)(x2-1) |
| 2(64k2-12) |
| 3+4k2 |
| 160k2 |
| 3+4k2 |
∴kNA=-kNB.
当x1=1或x2=1时,k=±1,
此时,对方程(*),△=0,不合题意.
∴直线AN与直线BN的倾斜角互补.
点评:本题考查圆的方程和椭圆方程的求法,考查两直线的倾斜角互补的证明,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
下列函数中,x=0是极值点的函数是( )
| A、y=-x3 | ||
| B、y=-cosx | ||
| C、y=tanx-x | ||
D、y=
|