题目内容
10.如果$sinx+cosx=-\frac{1}{5}$,且0<x<π,那么sinx-cosx的值是( )| A. | $\frac{7}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{7}{5}$ |
分析 两边平方得2sinxcosx=-$\frac{24}{25}$,结合x的范围可得cosx<0,由(sinx-cosx)2=$\frac{49}{25}$,即解得sinx-cosx的值.
解答 解:∵sinx+cosx=-$\frac{1}{5}$(0<x<π),
∴两边平方得2sinxcosx=-$\frac{24}{25}$,可得:cosx<0
∴(sinx-cosx)2=1-2sinxcosx=$\frac{49}{25}$,
∵sinx-cosx>0,
∴sinx-cosx=$\frac{7}{5}$.
故选:A.
点评 本题主要考查了同角三角函数的基本关系的应用.解题的过程中要特别注意根据角的范围确定三角函数值的正负号.

练习册系列答案
相关题目
11.设各项均为正数的等比数列{an}的公比为q,若数列{log2a1an}为递减数列,则( )
| A. | 0<q<1 | B. | q>1 | C. | 0<a1q<1 | D. | a1q>1 |
2.已知正四面体ABCD的棱长为a,其外接球表面积为S1,内切球表面积为S2,则S1:S2的值为( )
| A. | 3 | B. | $3\sqrt{3}$ | C. | 9 | D. | $\frac{49}{4}$ |
19.如图,网格纸上的小正方形边长都为4,粗线画出的是某几何体的三视图,则该几何体的体积为( )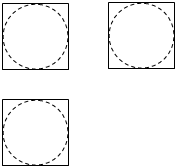

| A. | 64-$\frac{32}{3}$π | B. | 64-$\frac{96\sqrt{3}}{3}$π | C. | 64-$\frac{64\sqrt{2}}{3}$π | D. | 64-16π |
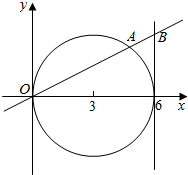 如图,已知动直线l交圆(x-3)2+y2=9于坐标原点O和点A,交直线x=6于点B;
如图,已知动直线l交圆(x-3)2+y2=9于坐标原点O和点A,交直线x=6于点B;