题目内容
19．如图，网格纸上的小正方形边长都为4，粗线画出的是某几何体的三视图，则该几何体的体积为（ ）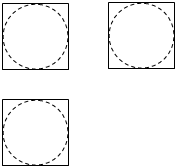
| A． | 64-$\frac{32}{3}$π | B． | 64-$\frac{96\sqrt{3}}{3}$π | C． | 64-$\frac{64\sqrt{2}}{3}$π | D． | 64-16π |
分析 由已知得该几何体是一个边长为4的正方体去掉它的内切球的剩余部分，由此能求出该几何体的体积．
解答 解：由已知得该几何体是一个边长为4的正方体去掉它的内切球的剩余部分，
∴该几何体的体积：
V=${4}^{3}-\frac{4}{3}π•{2}^{3}$=64-$\frac{32}{3}π$．
故选：A．
点评 本题考查几何体的求法，是基础题，解题时要认真审题，注意三视图性质的合理运用．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
10．如果$sinx+cosx=-\frac{1}{5}$，且0＜x＜π，那么sinx-cosx的值是（ ）
| A． | $\frac{7}{5}$ | B． | $\frac{4}{5}$ | C． | $-\frac{4}{5}$ | D． | $-\frac{7}{5}$ |
14．某几何体的三视图如图所示，则这个几何体的体积是（ ）
| A． | 4+8$\sqrt{2}$ | B． | 8+4$\sqrt{2}$ | C． | 4$\sqrt{2}$ | D． | 2$\sqrt{2}$ |
4．已知α是第二象限角，且sin（π-α）=$\frac{3}{5}$，则sin2α的值为（ ）
| A． | -$\frac{24}{25}$ | B． | $\frac{24}{25}$ | C． | -$\frac{7}{25}$ | D． | -$\frac{24}{7}$ |
11．已知点A（-1，0），B（3，2），则向量$\frac{1}{2}$$\overrightarrow{AB}$=（ ）
| A． | （2，2） | B． | （-1，1） | C． | （2，1） | D． | （-4，-2） |