题目内容
12.已知球O是的棱长为1的正方体ABCD-A1B1C1D1的内切球,则平面ACD1截球O的截面面积为( )| A. | π | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
分析 平面ACD1是边长为 $\sqrt{2}$的正三角形,且球与与以点D为公共点的三个面的切点恰为三角形ACD1三边的中点,从而得到所求截面的面积是该正三角形的内切圆的面积,由此能求出结果.
解答 解:根据题意知,平面ACD1是边长为 $\sqrt{2}$的正三角形,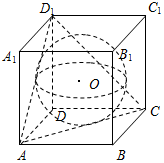
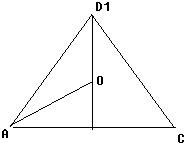
且球与与以点D为公共点的三个面的切点恰为三角形ACD1三边的中点,
故所求截面的面积是该正三角形的内切圆的面积,
则由图得,△ACD1内切圆的半径是$\frac{\sqrt{2}}{2}$×tan30°=$\frac{\sqrt{6}}{6}$,
则所求的截面圆的面积是π×$\frac{\sqrt{6}}{6}$×$\frac{\sqrt{6}}{6}$=$\frac{π}{6}$.
故选:D.
点评 本题考查平面截球的截面面积的求法,是中档题,解题时要认真审题,注意球、正方体的性质及构造法的合理应用.

练习册系列答案
相关题目
3.已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则(∁UA)∪B为( )
| A. | {1,2,4} | B. | {2,3,4} | C. | {0,2,4} | D. | {0,2,3,4} |
7.用0,1,2,3,4,5 组成没有重复的三位数,其中偶数共有( )
| A. | 24个 | B. | 30个 | C. | 52个 | D. | 60个 |
17.将边长为$\sqrt{2}$的正方形ABCD沿对角线AC折成一个直二面角B-AC-D.则四面体ABCD的内切球的半径为( )
| A. | 1 | B. | $2\sqrt{2}-\sqrt{3}$ | C. | $\sqrt{2}-1$ | D. | $2-\sqrt{3}$ |
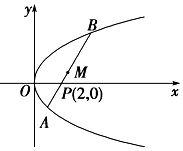 如图,已知直线l过点P(2,0),斜率为$\frac{4}{3}$,直线l和抛物线y2=2x相交于A、B两点,设线段AB的中点为M,求:
如图,已知直线l过点P(2,0),斜率为$\frac{4}{3}$,直线l和抛物线y2=2x相交于A、B两点,设线段AB的中点为M,求: