题目内容
17.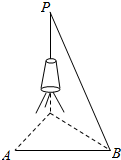 如图所示,要测量河对岸一电视塔的高PC,在河旁取A、B两点,测得AB=100$\sqrt{3}$米,∠CAB=∠ABC=60°,PB与地面所成的角为30°.
如图所示,要测量河对岸一电视塔的高PC,在河旁取A、B两点,测得AB=100$\sqrt{3}$米,∠CAB=∠ABC=60°,PB与地面所成的角为30°.(1)求电视塔的高PC;
(2)求异面直线PB与AC所成角的余弦值.
分析 (1)由已知得BC=AB=100$\sqrt{3}$,由此利用勾股定理能求出PC的长.
(2)以C为原点,CA为x轴,在平面ABC内过A作AC的垂线为y轴,以CP为z轴,建立空间直角坐标系,利用向量法能求出异面直线PB与AC所成角的余弦值.
解答 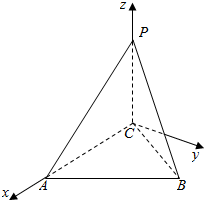 解:(1)∵AB=100$\sqrt{3}$米,∠CAB=∠ABC=60°,PB与地面所成的角为30°,PC⊥平面ABC,
解:(1)∵AB=100$\sqrt{3}$米,∠CAB=∠ABC=60°,PB与地面所成的角为30°,PC⊥平面ABC,
∴BC=AB=100$\sqrt{3}$,
设PC=x,则PB=2x,4x2-x2=(100$\sqrt{3}$)2,
解得x=100,即PC=100(米).
(2)以C为原点,CA为x轴,在平面ABC内过A作AC的垂线为y轴,以CP为z轴,
建立空间直角坐标系,
C(0,0,0),A(100$\sqrt{3}$,0,0),P(0,0,100),B(50$\sqrt{3}$,150,0),
$\overrightarrow{CA}$=(100$\sqrt{3}$,0,0),$\overrightarrow{PB}$=(50$\sqrt{3}$,150,-100),
设异面直线PB与AC所成角为θ,
cosθ=$\frac{|\overrightarrow{CA}•\overrightarrow{PB}|}{|\overrightarrow{CA}|•|\overrightarrow{PB}|}$=$\frac{|15000|}{100\sqrt{3}×\sqrt{40000}}$=$\frac{\sqrt{3}}{4}$.
∴异面直线PB与AC所成角的余弦值为$\frac{\sqrt{3}}{4}$.
点评 本题考查线段长的求法,考查异面直线所成角的余弦值的求法,是中档题,解题时要注意向量法的合理运用.

练习册系列答案
相关题目
8.下列说法正确的是( )
| A. | 命题“若sinx=siny,则x=y”的逆否命题为真命题 | |
| B. | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| C. | 命题“?x∈R,x2+x+1<0”的否定是“?x∈R,x2+x+1<0” | |
| D. | 命题“若x2=1,则x=1”的否命题为“若x2≠1,则x≠1” |
2.过点($\sqrt{3}$,-1)且与圆x2+y2=4相切的直线方程是( )
| A. | $\sqrt{3}$x+y-4=0 | B. | x-$\sqrt{3}$y-4=0 | C. | x-$\sqrt{3}$y-2=0 | D. | $\sqrt{3}$x-y-4=0 |