题目内容
11．
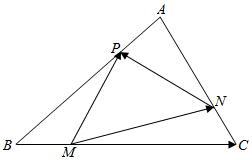如图，M、N、P分别是三角形ABC三边BC、CA、AB上的点，且满足$\frac{AP}{AB}=\frac{BM}{BC}=\frac{CN}{CA}=\frac{1}{4}$，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$．（1）用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{MN}$；
（2）若点G是三角形MNP的重心，用$\overrightarrow{a}$，$\overrightarrow{b}$表示$\overrightarrow{AG}$．
分析 （1）根据向量加法、减法及数乘的几何意义便可由条件及图形便可用$\overrightarrow{a}，\overrightarrow{b}$表示出$\overrightarrow{MN}=-\frac{3}{4}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$；
（2）先得出$\overrightarrow{MP}=\overrightarrow{MN}+\overrightarrow{NA}+\overrightarrow{AP}=-\frac{1}{2}\overrightarrow{a}-\frac{1}{4}\overrightarrow{b}$，然后画出图形，并连接AG，MG，根据G为三角形MNP的重心便可得到$\overrightarrow{MG}=-\frac{5}{12}\overrightarrow{a}+\frac{1}{12}\overrightarrow{b}$，从而根据$\overrightarrow{AG}=\overrightarrow{AP}+\overrightarrow{PM}+\overrightarrow{MG}$便可用$\overrightarrow{a}，\overrightarrow{b}$表示出$\overrightarrow{AG}$．
解答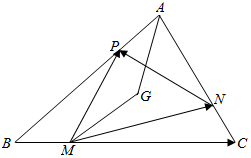 
解：（1）根据条件，$\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}$
=$\frac{3}{4}\overrightarrow{BC}+\frac{1}{4}\overrightarrow{CA}$
=$\frac{3}{4}（\overrightarrow{AC}-\overrightarrow{AB}）-\frac{1}{4}\overrightarrow{AC}$
=$-\frac{3}{4}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$
=$-\frac{3}{4}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$；
（2）$\overrightarrow{MP}=\overrightarrow{MN}+\overrightarrow{NA}+\overrightarrow{AP}$=$-\frac{3}{4}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}-\frac{3}{4}\overrightarrow{b}+\frac{1}{4}\overrightarrow{a}=-\frac{1}{2}\overrightarrow{a}-\frac{1}{4}\overrightarrow{b}$，如图，连接AG，MG；
G为三角形MNP的重心，则：$\overrightarrow{MG}=\frac{1}{3}（\overrightarrow{MN}+\overrightarrow{MP}）$=$\frac{1}{3}（-\frac{3}{4}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}-\frac{1}{2}\overrightarrow{a}-\frac{1}{4}\overrightarrow{b}）$=$-\frac{5}{12}\overrightarrow{a}+\frac{1}{12}\overrightarrow{b}$；
∴$\overrightarrow{AG}=\overrightarrow{AP}+\overrightarrow{PM}+\overrightarrow{MG}$
=$\frac{1}{4}\overrightarrow{a}+\frac{1}{2}\overrightarrow{a}+\frac{1}{4}\overrightarrow{b}-\frac{5}{12}\overrightarrow{a}+\frac{1}{12}\overrightarrow{b}$
=$\frac{1}{3}\overrightarrow{a}+\frac{1}{3}\overrightarrow{b}$．
点评 考查向量加法、减法及数乘的几何意义，向量的数乘运算，以及三角形重心的概念和性质，向量加法的平行四边形法则．
| A． | $\frac{3}{2}$$\sqrt{7}$ | B． | 4 | C． | $\frac{3\sqrt{5}}{2}$ | D． | 2$\sqrt{7}$ |
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{\sqrt{6}}{3}$ |
在市高三学业水平测试中，某校老师为了了解所教两个班100名学生的数学得分情况，按成绩分成六组：[80，90），[90，100），[100，110），[110，120），[120，130），[130，140）统计数据如下：| 分数段 | [80，90） | [90，100） | [100，110） | [110，120） | [120，130） | [130，140） |
| 人数 | 2 | 8 | 30 | 30 | 20 | 10 |
（Ⅱ）该教师决定在[110，120），[120，130），[130，140）这三组中用分层抽样抽取6名学生进行调研，然后再从这6名学生中随机抽取2名学生进行谈话，记这2名学生中有ξ名学生在[120，130）内，求ξ的分布列和数学期望．