题目内容
19.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$满足下列条件:①周期T=π;②图象向左平移$\frac{π}{6}$个单位长度后关于y轴对称; ③f(0)=1.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设α,β∈(0,$\frac{π}{4}$),f(α-$\frac{π}{3}$)=-$\frac{10}{13}$,f(β+$\frac{π}{6}$)=$\frac{6}{5}$,求cos(2α-2β)的值.
分析 (Ⅰ)根据f(x)的周期求出ω的值,根据f(x)的图象平移以及g(x)的图象关于y轴对称,求出φ的值,再由f(0)=1求出A的值,即得f(x)的解析式;
(Ⅱ)根据f(α-$\frac{π}{3}$)与f(β+$\frac{π}{6}$)的值求出cos2α、cos2β,再根据α、β的范围求出sin2α、sin2β,从而求出cos(2α-2β)的值.
解答 解:(Ⅰ)∵f(x)的周期为T=$\frac{2π}{ω}$=π,∴ω=2;
又函数f(x)的图象向左平移$\frac{π}{6}$个单位长度,
变为g(x)=Asin[2(x+$\frac{π}{6}$)+φ],
由题意,g(x)的图象关于y轴对称,
∴2×$\frac{π}{6}$+φ=$\frac{π}{2}$+kπ,k∈Z;
又|φ|<$\frac{π}{2}$,∴φ=$\frac{π}{6}$,
∴函数f(x)=Asin(2x+$\frac{π}{6}$);
又f(0)=1,∴Asin$\frac{π}{6}$=1,解得A=2,
∴函数f(x)=2sin(2x+$\frac{π}{6}$);
(Ⅱ)由f(α-$\frac{π}{3}$)=-$\frac{10}{13}$,f(β+$\frac{π}{6}$)=$\frac{6}{5}$,
得2sin(2α-$\frac{2π}{3}$+$\frac{π}{6}$)=-$\frac{10}{13}$,
2sin(2β+$\frac{π}{3}$+$\frac{π}{6}$)=$\frac{6}{5}$,
∴cos2α=$\frac{5}{13}$,cos2β=$\frac{3}{5}$;
又α、β∈(0,$\frac{π}{4}$),
∴2α、2β∈(0,$\frac{π}{2}$),
∴sin2α=$\frac{12}{13}$,sin2β=$\frac{4}{5}$,
∴cos(2α-2β)=cos2αcos2β+sin2αsin2β
=$\frac{5}{13}$×$\frac{3}{5}$+$\frac{12}{13}$×$\frac{4}{5}$=$\frac{63}{65}$.
点评 本题考查了三角函数的图象与性质的应用问题,也考查了三角函数的恒定变换应用问题,是基础题目.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | 45° | B. | 30° | C. | 75° | D. | 90° |
(I)求抽取的90名同学中的男生人数;
(Ⅱ)将下列2×2列联表补充完整,并判断能否在犯错误的概率不超过0.025的前提下认为“该校高一学生是否愿意选修英语口语课程与性别有关”?
| 愿意选修英语口语课程有效 | 不愿意选修英语口语课程 | 合计 | |
| 男生 | 25 | 25 | 50 |
| 女生 | 30 | 10 | 40 |
| 合计 | 55 | 35 | 90 |
| P(K2≥k0) | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
| A. | x=$\frac{π}{12}$ | B. | x=$\frac{5π}{12}$ | C. | x=$\frac{π}{6}$ | D. | x=$\frac{π}{3}$ |

| A. | n<5 | B. | n<6 | C. | n≤6 | D. | n<9 |
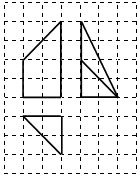 如图网格纸上小正方形的边长为l,粗实线画山的是某几何体的三视图,则这个几何体的体积为( )
如图网格纸上小正方形的边长为l,粗实线画山的是某几何体的三视图,则这个几何体的体积为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
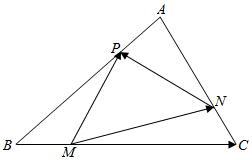 如图,M、N、P分别是三角形ABC三边BC、CA、AB上的点,且满足$\frac{AP}{AB}=\frac{BM}{BC}=\frac{CN}{CA}=\frac{1}{4}$,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.
如图,M、N、P分别是三角形ABC三边BC、CA、AB上的点,且满足$\frac{AP}{AB}=\frac{BM}{BC}=\frac{CN}{CA}=\frac{1}{4}$,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.