题目内容
20.已知${(x-\frac{1}{x})^n}$的展开式中第3项与第6项的二项式系数相等,则展开式中系数最大的项为第( )项.| A. | 5 | B. | 4 | C. | 4或5 | D. | 5或6 |
分析 利用二项式系数的性质求得n=7,再利用二项式展开式的通项公式求得第r+1项的系数,可得结论.
解答 解:由题意可得${C}_{n}^{2}$=${C}_{n}^{5}$,求得n=7,
故展开式第r+1项的系数为Tr+1=${C}_{7}^{r}$•(-1)r,故当r=4,即第五项的系数最大,
故选:A.
点评 本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.某校拟在高一年级开设英语口语选修课,该年级男生600人,女生480人.按性别分层抽样,抽取90名同学做意向调查.
(I)求抽取的90名同学中的男生人数;
(Ⅱ)将下列2×2列联表补充完整,并判断能否在犯错误的概率不超过0.025的前提下认为“该校高一学生是否愿意选修英语口语课程与性别有关”?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
(I)求抽取的90名同学中的男生人数;
(Ⅱ)将下列2×2列联表补充完整,并判断能否在犯错误的概率不超过0.025的前提下认为“该校高一学生是否愿意选修英语口语课程与性别有关”?
| 愿意选修英语口语课程有效 | 不愿意选修英语口语课程 | 合计 | |
| 男生 | 25 | 25 | 50 |
| 女生 | 30 | 10 | 40 |
| 合计 | 55 | 35 | 90 |
| P(K2≥k0) | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
8.已知AB为圆O:(x-1)2+y2=1的直径,点P为直线x-y+1=0上任意一点,则$\overrightarrow{PA}•\overrightarrow{PB}$的最小值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
15.已知$sin(x+\frac{π}{6})=\frac{1}{3}$,则$sin(x-\frac{5π}{6})+{sin^2}(\frac{π}{3}-x)$的值是$\frac{5}{9}$.
12.${(x-\frac{a}{x})^5}(x∈R)$展开式中x3的系数为10,则实数a的值为( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | -2 |
10.已知方程(x2-mx+4)(x2-nx+4)=0的四个根组成一个首项$\frac{1}{4}$的等比数列,则|m-n|的值为( )
| A. | 0 | B. | $11\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
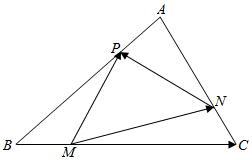 如图,M、N、P分别是三角形ABC三边BC、CA、AB上的点,且满足$\frac{AP}{AB}=\frac{BM}{BC}=\frac{CN}{CA}=\frac{1}{4}$,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.
如图,M、N、P分别是三角形ABC三边BC、CA、AB上的点,且满足$\frac{AP}{AB}=\frac{BM}{BC}=\frac{CN}{CA}=\frac{1}{4}$,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$.