题目内容
6.点D是△ABC中AB边的中点,CA=CB,E是CD的中点,AE的延长线交BC于F,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{DC}$=$\overrightarrow{b}$,则$\overrightarrow{AF}$=( )| A. | $\frac{1}{4}$$\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\frac{1}{2}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}\overrightarrow{b}$ |
分析 可画出图形,由条件及图形便可得出$\overrightarrow{AE}=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$,$\overrightarrow{AF}$与$\overrightarrow{AE}$共线,从而得到$\overrightarrow{AF}=\frac{k}{2}\overrightarrow{a}+\frac{k}{2}\overrightarrow{b}$,而由B,F,C三点共线便可以得出$\overrightarrow{AF}=λ\overrightarrow{AB}+(1-λ)\overrightarrow{AC}=\frac{1+λ}{2}\overrightarrow{a}+(1-λ)\overrightarrow{b}$,从而根据平面向量基本定理便可得出$\frac{1+λ}{2}=1-λ$,这样即可解出λ,从而可用$\overrightarrow{a},\overrightarrow{b}$表示出$\overrightarrow{AF}$.
解答 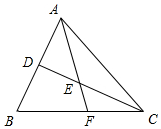 解:如图,根据条件:
解:如图,根据条件:
$\overrightarrow{AE}=\overrightarrow{AD}+\overrightarrow{DE}=\overrightarrow{AD}+\frac{1}{2}\overrightarrow{DC}$=$\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{DC}=\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$;
∴$\overrightarrow{AF}=k\overrightarrow{AE}=\frac{k}{2}\overrightarrow{a}+\frac{k}{2}\overrightarrow{b}$;
B,F,C三点共线,∴$\overrightarrow{AF}=λ\overrightarrow{AB}+(1-λ)\overrightarrow{AC}$=$λ\overrightarrow{AB}+(1-λ)(\frac{1}{2}\overrightarrow{AB}+\overrightarrow{DC})$=$\frac{1+λ}{2}\overrightarrow{AB}+(1-λ)\overrightarrow{DC}=\frac{1+λ}{2}\overrightarrow{a}+(1-λ)\overrightarrow{b}$;
∴$\frac{1+λ}{2}=1-λ$;
解得$λ=\frac{1}{3}$;
∴$\overrightarrow{AF}=\frac{2}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}$.
故选:C.
点评 考查向量加法和数乘的几何意义,以及向量的数乘运算,共线向量基本定理,平面向量基本定理.

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
| A. | 8π | B. | 16π | C. | $\frac{8π}{3}$ | D. | $\frac{16π}{3}$ |
| A. | {a|a≤0} | B. | {a|0≤a≤1} | C. | {a|a=1} | D. | {a|a=-1} |