题目内容
11.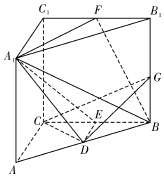 如图,三棱柱ABC-A1B1C1中,∠ACB=90°,CC1⊥底面ABC,AC=BC=CC1=2,D,E,F分别是棱AB,BC,B1C1的中点,G是棱BB1上的动点.
如图,三棱柱ABC-A1B1C1中,∠ACB=90°,CC1⊥底面ABC,AC=BC=CC1=2,D,E,F分别是棱AB,BC,B1C1的中点,G是棱BB1上的动点.(1)当$\frac{BG}{{B{B_1}}}$为何值时,平面CDG⊥平面A1DE?
(2)求平面AB1F与平面AD1E所成的锐二面角的余弦值.
分析 (1)当G为BB1中点(即$\frac{BG}{{B{B_1}}}=\frac{1}{2}$)时,平面CDG⊥平面A1DE.证明D,E,C1,A1四点共面.连接C1E交GC于H.证明CG⊥C1E.DE⊥CG,推出CG⊥平面A1DE,即可证明平面CDG⊥平面A1DE.
(2)以C为原点,CA,CB,CC1所在的直线分别为x,y,z轴建立空间直角坐标系,求出平面A1DE的法向量,平面A1BF的法向量,设平面A1BF与平面A1DE所成的锐二面角为θ,利用数量积求解即可.
解答 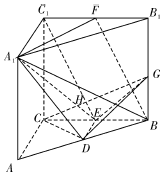 解:(1)当G为BB1中点(即$\frac{BG}{{B{B_1}}}=\frac{1}{2}$)时,平面CDG⊥平面A1DE.
解:(1)当G为BB1中点(即$\frac{BG}{{B{B_1}}}=\frac{1}{2}$)时,平面CDG⊥平面A1DE.
证明如下:由于DE∥AC且$DE=\frac{1}{2}AC,AC∥{A_1}{C_1},AC={A_1}{C_1}$,∴$DE∥{A_1}{C_1},DE=\frac{1}{2}{A_1}{C_1}$,故D,E,C1,A1四点共面.
连接C1E交GC于H.在正方形CBB1C1中,$tan∠{C_1}EC=2,tan∠BCG=\frac{1}{2}$,故∠CHE=90°,即CG⊥C1E.又A1C1⊥平面CBB1C1,CG?平面CBB1C1,所以DE⊥CG,又因为C1E∩DE=E,故CG⊥平面A1DE,从而平面CDG⊥平面A1DE.
(2)三棱柱ABC-A1B1C1中,∠ACB=90°,CC1⊥底面ABC,
于是可以以C为原点,CA,CB,CC1所在的直线分别为x,y,z轴建立空间直角坐标系,
如图所示.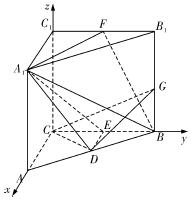
因为AC=BC=CC1=2,D,E,F分别是棱AB,BC,B1C1的中点,
所以A1(2,0,2),D(1,1,0),E(0,1,0),B(0,2,0),F(0,1,2),
G(0,2.1),$\overrightarrow{{A}_{1}B}$=(-2,2,-2),$\overrightarrow{{A}_{1}F}$=(-2,1,0).
由(1)知平面A1DE的法向量为$\overrightarrow{CG}$=(0,2,1),
设平面A1BF的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{A}_{1}F}=0}\\{\overrightarrow{n}•\overrightarrow{{A}_{1}B}=0}\end{array}\right.$,即:$\left\{\begin{array}{l}{-2x+y=0}\\{-2x+2y-2z=0}\end{array}\right.$,
令x=1得$\overrightarrow n=({1,2,1})$,
设平面A1BF与平面A1DE所成的锐二面角为θ,
则cosθ=$\frac{|\overrightarrow{CG}•\overrightarrow{n}|}{|\overrightarrow{CG}||\overrightarrow{n}|}$=$\frac{5}{\sqrt{30}}$=$\frac{\sqrt{30}}{6}$.
点评 本题考查直线与平面垂直的判定定理以及平面与平面垂直的判定定理的应用,二面角的平面角的求法,考查空间想象能力以及计算能力.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案| A. | $\frac{8}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{5}$ |
| A. | 5 | B. | 5+4i | C. | -3 | D. | 3-4i |
| A. | (-∞,0) | B. | $(0,\frac{1}{2})$ | C. | $(\frac{1}{2},1)$ | D. | (1,+∞) |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |