题目内容
3.已知定义在R上的函数f(x)=ex+mx2-m(m>0),当x1+x2=1时,不等式f(x1)+f(0)>f(x2)+f(1)恒成立,则实数x1的取值范围是( )| A. | (-∞,0) | B. | $(0,\frac{1}{2})$ | C. | $(\frac{1}{2},1)$ | D. | (1,+∞) |
分析 通过变形可知问题转化为不等式f(x1)-f(1-x1)>f(1)-f(1-1)恒成立,设g(x)=f(x)-f(1-x)并求导可知g(x)在R上单调递增,利用单调性即得结论.
解答 解:∵不等式f(x1)+f(0)>f(x2)+f(1)恒成立,
∴不等式f(x1)-f(x2)>f(1)-f(0)恒成立,
又∵x1+x2=1,
∴不等式f(x1)-f(1-x1)>f(1)-f(1-1)恒成立,
设g(x)=f(x)-f(1-x),
∵f(x)=ex+mx2-m(m>0),
∴g(x)=ex-e1-x+m(2x-1),
则g′(x)=ex+e1-x+2m>0,∴g(x)在R上单调递增,
∴不等式g(x1)>g(1)恒成立,
∴x1>1,
故选:D.
点评 本题是一道关于导数的综合题,考查转化与化归思想,构造新函数是解决本题的关键,注意解题方法的积累,属于难题.

练习册系列答案
相关题目
14.在高中学习过程中,同学们经常这样说:“数学物理不分家,如果物理成绩好,那么学习数学就没什么问题.”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了苏俄生的物理成绩与数学成绩具有线性相关关系的结论.现从该班随机抽取5名学生在一次考试中的数学和物理成绩,如表:
(1)求数学成绩y对物理成绩x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$($\widehat{b}$精确到0.1).若某位学生的物理成绩为80分,预测他的数学成绩;
(2)要从抽取的这五位学生中随机选出2位参加一项知识竞赛,求选中的学生的数学成绩至少有一位高于120分的概率.(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
(参考数据:902+852+742+682+632=29394,90××125+74×110+68×95+63×90=42595)
| 成绩 编号 | 1 | 2 | 3 | 4 | 5 |
| 物理(x) | 90 | 85 | 74 | 68 | 63 |
| 数学(y) | 130 | 125 | 110 | 95 | 90 |
(2)要从抽取的这五位学生中随机选出2位参加一项知识竞赛,求选中的学生的数学成绩至少有一位高于120分的概率.(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
(参考数据:902+852+742+682+632=29394,90××125+74×110+68×95+63×90=42595)
18.设a,b均为实数,则“a>|b|”是“a3>b3”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.已知复数z(1+4i)=2i-5(i为虚数单位),则复数z的虚部为( )
| A. | -$\frac{22}{17}$ | B. | $\frac{22}{17}$i | C. | $\frac{22}{17}$ | D. | $\frac{3}{17}$ |
12.已知函数$f(x)=\left\{{\begin{array}{l}{2x-xlnx(x>0)}\\{-{x^2}-\frac{3}{2}x(x≤0)}\end{array}}\right.$有且仅有四个不同的点关于直线y=1的对称点在直线kx+y-1=0上,则实数k的取值范围为( )
| A. | $(\frac{1}{2},1)$ | B. | $(\frac{1}{2},\frac{3}{4})$ | C. | $(\frac{1}{3},1)$ | D. | $(\frac{1}{2},2)$ |
13.“sinα+cosα=0”是“cos2α=0”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分且必要条件 | D. | 既不充分也不必要条件 |
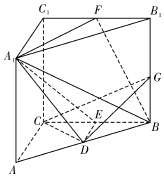 如图,三棱柱ABC-A1B1C1中,∠ACB=90°,CC1⊥底面ABC,AC=BC=CC1=2,D,E,F分别是棱AB,BC,B1C1的中点,G是棱BB1上的动点.
如图,三棱柱ABC-A1B1C1中,∠ACB=90°,CC1⊥底面ABC,AC=BC=CC1=2,D,E,F分别是棱AB,BC,B1C1的中点,G是棱BB1上的动点.