题目内容
1.已知θ的终边过点P(-12,5),则cosθ=$-\frac{12}{13}$.分析 先求出θ的终边上点P(-12,5)到原点的距离为r,再利用任意角的三角函数的定义求出结果.
解答 解:∵θ的终边过点P(-12,5),
∴x=-12,y=5,∴r=13,
由任意角的三角函数的定义得cosα=$\frac{x}{r}$=-$-\frac{12}{13}$.
故答案为:$-\frac{12}{13}$.
点评 本题考查任意角的三角函数的定义,两点间的距离公式的应用.

练习册系列答案
相关题目
11.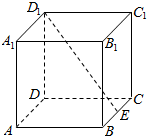 如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )
如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )
 如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )
如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )| A. | $\frac{{4\sqrt{5}}}{5}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 3 |
9.函数f(x)=$\sqrt{1-x}$+lg(3x+1)的定义域是( )
| A. | $(-\frac{1}{3},+∞)$ | B. | $(-\frac{1}{3},1)$ | C. | $(-\frac{1}{3},1]$ | D. | $(\frac{1}{3},1)$ |
7.已知正方体ABCD-A1B1C1D1的棱长为1,M为棱CC1的中点,则点M到平面A1BD的距离是( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
8.已知a,b∈R,且ab≠0,那么“a>b”是“lg(a-b)>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
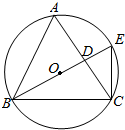 如图,点E在△ABC的外接圆O上,AB=AC,$\widehat{AE}$=$\widehat{CE}$,AC交BE于点D,圆O的面积为S.
如图,点E在△ABC的外接圆O上,AB=AC,$\widehat{AE}$=$\widehat{CE}$,AC交BE于点D,圆O的面积为S.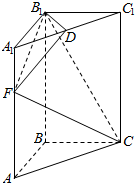 如图,高为3的直三棱柱ABC-A1B1C1中,底面是直角三角形,AC=2,D为A1C1的中点,F在线段AA1上,CF⊥DB1,且A1F=1.
如图,高为3的直三棱柱ABC-A1B1C1中,底面是直角三角形,AC=2,D为A1C1的中点,F在线段AA1上,CF⊥DB1,且A1F=1.