题目内容
6.已知双曲线$\frac{x^2}{4}$-$\frac{y^2}{b^2}$=1(b>0)的离心率等于$\frac{\sqrt{3}}{3}$b,则该双曲线的焦距为( )| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{6}$ | C. | 6 | D. | 8 |
分析 设双曲线$\frac{x^2}{4}$-$\frac{y^2}{b^2}$=1(b>0)的焦距为2c,根据双曲线的几何性质求出c的值即可得焦距.
解答 解:设双曲线$\frac{x^2}{4}$-$\frac{y^2}{b^2}$=1(b>0)的焦距为2c,
由已知得,a=2;
又离心率e=$\frac{c}{2}$=$\frac{\sqrt{3}}{3}$b,
且c2=4+b2,
解得c=4;
所以该双曲线的焦距为2c=8.
故选:D.
点评 本题考查了双曲线的定义与简单几何性质的应用问题,是基础题目.

练习册系列答案
相关题目
10.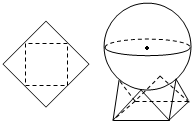 用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,现将半径为$\sqrt{2}$的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为( )
用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,现将半径为$\sqrt{2}$的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为( )
 用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,现将半径为$\sqrt{2}$的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为( )
用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,现将半径为$\sqrt{2}$的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为( )| A. | $\frac{\sqrt{2}+2}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | C. | $\frac{\sqrt{10}+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{10}-\sqrt{2}}{2}$ |
11.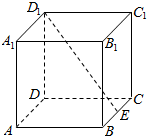 如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )
如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )
 如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )
如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )| A. | $\frac{{4\sqrt{5}}}{5}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 3 |
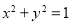 上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线
上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线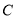 .
.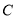 的参数方程;
的参数方程;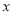 轴正半轴为极轴坐标建立极坐标系,已知直线
轴正半轴为极轴坐标建立极坐标系,已知直线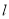 的极坐标方程为
的极坐标方程为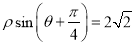 ,若
,若 分别为曲线
分别为曲线 和直线
和直线 上的一点,求
上的一点,求 的最近距离.
的最近距离.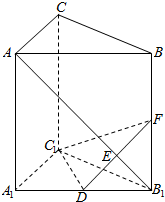 如图,直三棱柱ABC一A1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E,要使AB1⊥平面C1DF,则线段B1F的长为$\frac{1}{2}$.
如图,直三棱柱ABC一A1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E,要使AB1⊥平面C1DF,则线段B1F的长为$\frac{1}{2}$.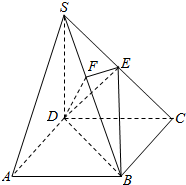 如图,在四棱锥S-ABCD中,底面ABCD是矩形,SD=DC=2AD,侧棱SD⊥底面ABCD,点E是SC的中点,点F在SB上,且EF⊥SB.
如图,在四棱锥S-ABCD中,底面ABCD是矩形,SD=DC=2AD,侧棱SD⊥底面ABCD,点E是SC的中点,点F在SB上,且EF⊥SB.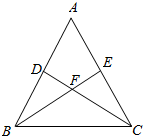 如图,在△ABC中,DC⊥AB于D,BE⊥AC于E,BE交DC于点F,若BF=FC=3,DF=FE=2.
如图,在△ABC中,DC⊥AB于D,BE⊥AC于E,BE交DC于点F,若BF=FC=3,DF=FE=2.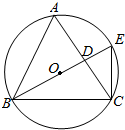 如图,点E在△ABC的外接圆O上,AB=AC,$\widehat{AE}$=$\widehat{CE}$,AC交BE于点D,圆O的面积为S.
如图,点E在△ABC的外接圆O上,AB=AC,$\widehat{AE}$=$\widehat{CE}$,AC交BE于点D,圆O的面积为S.