题目内容
14.从装有3个红球和3个白球的口袋里任取3个球,那么互斥而不对立的两个事件是( )| A. | 至少2个白球,都是红球 | B. | 至少1个白球,至少1个红球 | ||
| C. | 至少2个白球,至多1个白球 | D. | 恰好1个白球,恰好2个红球 |
分析 分析出从装有3个红球和3个白球的口袋内任取3个球的所有不同情况,然后利用互斥事件和对立事件的概念逐一核对四个选项即可得到答案.
解答 解:从装有3个红球和3个白球的口袋内任取3个球,
取球情况有:3个球都是红球;3个球中1个红球2个白球;
3个球中2个红球1个白球;3个球都是白球.
选项A中“至少2个白球“,与”都是红球“互斥而不对立,
选项B中“至少有一个白球”与“至少有一个红球”的交事件是“有1白球2个红球”或“有2白球1个红球”;
选项C中“至少有2个白球”与“至多1个白球”是对立事件;
选项D中“恰有一个白球”和“恰有两个红球”既不互斥也不对立.
故选:A.
点评 本题考查了互斥事件和对立事件的概念,对于两个事件而言,互斥不一定对立,对立必互斥,是基础的概念题.

练习册系列答案
相关题目
19.已知点A(-2,3)在抛物线C:y2=2px的准线上,记C的焦点为F,则直线AF的斜率为( )
| A. | -2 | B. | -$\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{1}{2}$ |
9.函数$f(x)=\frac{x^3}{3}+\frac{1}{x}$的导数f'(x)=( )
| A. | $\frac{x^2}{3}+\frac{1}{x}$ | B. | ${x^2}-\frac{1}{x^2}$ | C. | $-{x^2}-\frac{1}{x^2}$ | D. | x2+lnx |
19.函数$y=sin({x+\frac{π}{3}})$的图象( )
| A. | 对称关于点$(\frac{π}{6},0)$对称 | B. | 关于直线$x=\frac{π}{6}$ | ||
| C. | 关于y轴对称 | D. | 关于原点对称 |
3.已知函数f(x)=Asin(ωx+φ)( A>0,ω>0,$|φ|<\frac{π}{2}$)在一个周期内的图象如图所示,则$f({\frac{π}{6}})$=( )
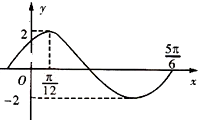

| A. | 1 | B. | $\sqrt{3}$ | C. | -1 | D. | $-\sqrt{3}$ |
4.已知f(sin x)=cos 3x,则f(cos 10°)的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |