题目内容
4.已知f(sin x)=cos 3x,则f(cos 10°)的值为( )| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 cos 10°=sin80°,由f(sin x)=cos 3x,可得f(cos 10°)=f(sin80°)=cos 3×80°=cos240°.可得答案.
解答 解:∵cos 10°=sin80°,
由题意,f(sin x)=cos 3x,
可得f(cos 10°)=f(sin80°)=cos 3×80°=cos240°=$-\frac{1}{2}$,
故选:A.
点评 本题考查了诱导公式的运用和转化思想.属于基础题

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
14.从装有3个红球和3个白球的口袋里任取3个球,那么互斥而不对立的两个事件是( )
| A. | 至少2个白球,都是红球 | B. | 至少1个白球,至少1个红球 | ||
| C. | 至少2个白球,至多1个白球 | D. | 恰好1个白球,恰好2个红球 |
12.已知函数f(x),g(x)满足f(1)=1,f'(1)=1,g(1)=2,g'(1)=1,则函数F(x)=$\frac{f(x)^{2}}{g(x)}$的图象在x=1处的切线方程为( )
| A. | 3x-4y+5=0 | B. | 3x-4y-1=0. | C. | 4x-3y-5=0 | D. | 4x-3y+5=0 |
19.抛物线x2=ay上有一点A(x0,2),它到焦点的距离是3,则其标准方程是( )
| A. | x2=y | B. | x2=2y | C. | x2=3y | D. | x2=4y |
9.下列说法中正确的是( )
| A. | 第一象限角一定是正角 | B. | 终边与始边均相同的角一定相等 | ||
| C. | -834°是第四象限角 | D. | 钝角一定是第二象限角 |
14.某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差xi与实验室每天每100颗种子浸泡后的发芽数yi(i=1,2,…,5),作了初步处理,得到下表:
(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为m,n,求事件“m,n均小于26”的概率;
(2)请根据3月1日至3月5日的数据,求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,并预报3月份昼夜温差为14度时实验室每天100颗种子浸泡后的发芽(取整数值).
附:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的斜率和截距最小二乘法估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,$\sum_{i=1}^5{{x_i}{y_i}=1351}$,$\sum_{i=1}^5{x_i^2}$=615.
| 日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
| 温差xi(0C) | 10 | 11 | 13 | 12 | 9 |
| 发芽率yi(颗) | 23 | 25 | 30 | 26 | 16 |
(2)请根据3月1日至3月5日的数据,求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,并预报3月份昼夜温差为14度时实验室每天100颗种子浸泡后的发芽(取整数值).
附:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中的斜率和截距最小二乘法估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,$\sum_{i=1}^5{{x_i}{y_i}=1351}$,$\sum_{i=1}^5{x_i^2}$=615.
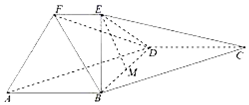 在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥面ABCD,EF∥AB,AB=2,EB=$\sqrt{3}$的中点.
在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥面ABCD,EF∥AB,AB=2,EB=$\sqrt{3}$的中点.