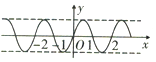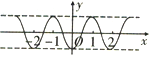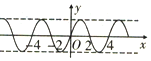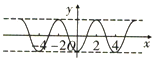题目内容
19.函数$y=sin({x+\frac{π}{3}})$的图象( )| A. | 对称关于点$(\frac{π}{6},0)$对称 | B. | 关于直线$x=\frac{π}{6}$ | ||
| C. | 关于y轴对称 | D. | 关于原点对称 |
分析 根据三角函数$y=sin({x+\frac{π}{3}})$的图象与性质,对选项中的命题分析、判断正误即可.
解答 解:对于A,x=$\frac{π}{6}$时,y=sin($\frac{π}{6}$+$\frac{π}{3}$)=1,
∴函数$y=sin({x+\frac{π}{3}})$的图象不关于点($\frac{π}{6}$,0)对称,A错误;
对于B,x=$\frac{π}{6}$时,y=sin($\frac{π}{6}$+$\frac{π}{3}$)=1,
∴函数$y=sin({x+\frac{π}{3}})$的图象关于直线x=$\frac{π}{6}$对称,B正确;
对于C,x=0时,y=sin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$≠1,
∴函数$y=sin({x+\frac{π}{3}})$的图象不关于y轴对称,C错误;
对于D,x=0时,y=sin$\frac{π}{3}$=$\frac{\sqrt{3}}{2}$≠0,
∴函数$y=sin({x+\frac{π}{3}})$的图象不关于原点对称,D错误.
故选:B.
点评 本题考查了三角函数的图象与性质的应用问题,是基础题.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
14.从装有3个红球和3个白球的口袋里任取3个球,那么互斥而不对立的两个事件是( )
| A. | 至少2个白球,都是红球 | B. | 至少1个白球,至少1个红球 | ||
| C. | 至少2个白球,至多1个白球 | D. | 恰好1个白球,恰好2个红球 |
9.下列说法中正确的是( )
| A. | 第一象限角一定是正角 | B. | 终边与始边均相同的角一定相等 | ||
| C. | -834°是第四象限角 | D. | 钝角一定是第二象限角 |
 如图,已知菱形ABEF所在的平面与△ABC所在的平面相互垂直,AB=4,BC=$\sqrt{6}$,BC⊥BE,∠ABE=$\frac{π}{3}$.
如图,已知菱形ABEF所在的平面与△ABC所在的平面相互垂直,AB=4,BC=$\sqrt{6}$,BC⊥BE,∠ABE=$\frac{π}{3}$.