题目内容

19．已知点A（-2，3）在抛物线C：y2=2px的准线上，记C的焦点为F，则直线AF的斜率为（　　）
A．-2B．-$\frac{4}{3}$C．-$\frac{3}{4}$D．-$\frac{1}{2}$

分析 由题意求得抛物线方程，求得焦点坐标，利用直线的斜率公式即可求得直线AF的斜率．

解答 解：由点A（-2，3）在抛物线C：y2=2px的准线上，
即-2=-$\frac{p}{2}$，则p=4，
故抛物线的焦点坐标为：（2，0），
则直线AF的斜率k=$\frac{3-0}{-2-2}$=-$\frac{3}{4}$，
故选C．

点评 本题考查抛物线的简单几何性质，抛物线的焦点坐标及准线方程，考查计算能力，属于基础题．

练习册系列答案
相关题目
9．已知函数f（x）=x3+x．
（1）求定积分$\int_{-3}^3{（{f（x）+{x^2}}）dx}$的值；
（2）若曲线y=f（x）的一条切线经过点（0，-2），求此切线的方程．
10．如图，在平面四边形ABCD中，AD=1，CD=2，AC=$\sqrt{7}$．cos∠BAD=-$\frac{\sqrt{7}}{14}$，sin∠CBA=$\frac{\sqrt{21}}{6}$，则BC的长为（　　）
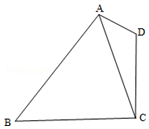
A．$\sqrt{7}$B．2C．3D．2$\sqrt{7}$
7．函数$y=tan（\frac{π}{4}-x）$的定义域是（　　）
A．{x|x≠$\frac{π}{4}$，k∈Z x∈R}B．{x|x≠kπ$+\frac{π}{4}$，k∈Z，x∈R}
C．{x|x≠$-\frac{π}{4}$，k∈Z x∈R}D．{x|x≠kπ$+\frac{3}{4}π$，k∈Z，x∈R}
14．设函数f（x）=-$\frac{1}{3}$x3+ax2+bx+ab，x∈R，其中a，b∈R．
（Ⅰ）若函数f（x）在x=1处有极小值-$\frac{22}{3}$，求a．b的值；
（Ⅱ）若|a|＞1，设g（x）=|f′（x）|，求证：当x∈[-1，1]时，g（x）max＞2；
（Ⅲ）若a＞1，b＜1-2a，对于给定x1，x2∈（-∞，1），x1＜x2，α=mx1+（1-m）x2，β=（1-m）x1+mx2，其中m∈R，α＜1，β＜1，若|f（α）-f（β）|＜|f（x1）-f（x2）|，求m的取值范围．
4．袋中装有黑球和白球共7个，从中任取2个球都是白球的概率为$\frac{1}{7}$，现有甲、乙两人从袋中轮流摸取1球，甲先取，乙后取，然后甲再取，…，取后不放回，直到两人中有一人取到白球时即终止，每个球在每一次被取出的机会是等可能的．
（Ⅰ）求袋中原有白球的个数；
（Ⅱ）求取球次数X的分布列和数学期望．
11．设向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1，$\overrightarrow{a}$•$\overrightarrow{b}$=-$\frac{1}{4}$，则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=2．
13．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}，x≤0}\\{lo{g}_{2}x，x＞0}\end{array}\right.$，则方程$f（x）=\frac{1}{2}$的解集为（　　）
A．$\{\sqrt{2}，-\frac{{\sqrt{2}}}{2}，\frac{{\sqrt{2}}}{2}\}$B．$\{\sqrt{2}，\frac{{\sqrt{2}}}{2}\}$C．$\{-\frac{{\sqrt{2}}}{2}，\frac{{\sqrt{2}}}{2}\}$D．$\{\sqrt{2}，-\frac{{\sqrt{2}}}{2}\}$
14．从装有3个红球和3个白球的口袋里任取3个球，那么互斥而不对立的两个事件是（　　）
A．至少2个白球，都是红球B．至少1个白球，至少1个红球
C．至少2个白球，至多1个白球D．恰好1个白球，恰好2个红球

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网