题目内容
3.已知函数f(x)=Asin(ωx+φ)( A>0,ω>0,$|φ|<\frac{π}{2}$)在一个周期内的图象如图所示,则$f({\frac{π}{6}})$=( )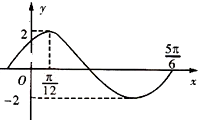
| A. | 1 | B. | $\sqrt{3}$ | C. | -1 | D. | $-\sqrt{3}$ |
分析 由图知,A=2,易求T=π,ω=2,由f($\frac{π}{12}$)=2,|φ|<$\frac{π}{2}$,可求得φ=$\frac{π}{3}$,从而可得函数y=f(x)的解析式,继而得f($\frac{π}{6}$)的值.
解答 解:由图知,A=2,且$\frac{3}{4}$T=$\frac{5π}{6}$-$\frac{π}{12}$=$\frac{3π}{4}$,
∴T=π,ω=2.
∴f(x)=2sin(2x+φ),
又f($\frac{π}{12}$)=2,
∴sin(2×$\frac{π}{12}$+φ)=1,
∴$\frac{π}{6}$+φ=2kπ+$\frac{π}{2}$(k∈Z),又|φ|<$\frac{π}{2}$,
∴φ=$\frac{π}{3}$,
∴f(x)=2sin(2x+$\frac{π}{3}$),
∴f($\frac{π}{6}$)=2sin$\frac{2π}{3}$=$\sqrt{3}$,
故选:B.
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求φ是难点,考查识图与运算能力,属于基础题.

练习册系列答案
相关题目
13.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2},x≤0}\\{lo{g}_{2}x,x>0}\end{array}\right.$,则方程$f(x)=\frac{1}{2}$的解集为( )
| A. | $\{\sqrt{2},-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}\}$ | B. | $\{\sqrt{2},\frac{{\sqrt{2}}}{2}\}$ | C. | $\{-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}\}$ | D. | $\{\sqrt{2},-\frac{{\sqrt{2}}}{2}\}$ |
14.从装有3个红球和3个白球的口袋里任取3个球,那么互斥而不对立的两个事件是( )
| A. | 至少2个白球,都是红球 | B. | 至少1个白球,至少1个红球 | ||
| C. | 至少2个白球,至多1个白球 | D. | 恰好1个白球,恰好2个红球 |
18.已知A(-1,2),B(-2,4),则直线AB的斜率为( )
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
12.已知函数f(x),g(x)满足f(1)=1,f'(1)=1,g(1)=2,g'(1)=1,则函数F(x)=$\frac{f(x)^{2}}{g(x)}$的图象在x=1处的切线方程为( )
| A. | 3x-4y+5=0 | B. | 3x-4y-1=0. | C. | 4x-3y-5=0 | D. | 4x-3y+5=0 |
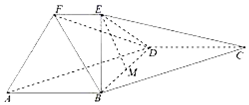 在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥面ABCD,EF∥AB,AB=2,EB=$\sqrt{3}$的中点.
在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥面ABCD,EF∥AB,AB=2,EB=$\sqrt{3}$的中点.