题目内容
直线kx-y+6=0被圆x2+y2=25截得的弦长为8，求k的值．
考点：直线和圆的方程的应用
专题：计算题,直线与圆
分析：利用垂径定理及勾股定理即可求出弦长，利用点到直线的距离公式求出圆心到直线的距离d，从而可得结论．
解答：
解：∵直线kx-y+6=0被圆x2+y2=25截得的弦长为8，
∴弦心距为
=3．
∴
=3，
解得k=±
．
∴弦心距为
| 52-42 |
∴
| |k•0-0+6| | ||
|
解得k=±
| 3 |
点评：此题考查了直线与圆相交的性质，涉及的知识有：圆的标准方程，点到直线的距离公式，垂径定理及勾股定理，熟练掌握定理及公式是解本题的关键．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
在平面直角坐标系中，直线x-y=0与曲线y=x2-2x所围成的面积为（ ）
| A、1 | ||
B、
| ||
C、
| ||
| D、9 |
已知圆C：（x-2）2+（y+1）2=3，从点P（-1，-3）发出的光线，经x轴反射后恰好经过圆心C，则入射光线的斜率为（ ）
A、-
| ||
B、-
| ||
C、
| ||
D、
|
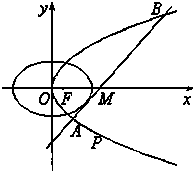已知椭圆C1和抛物线C2有公共焦点F（1，0），C1的中心和C2的顶点都在坐标原点，过点M（4，0）的直线l与抛物线C2分别相交于A，B两点．
如图，⊙O为四边形ABCD的外接圆，且AB=AD，E是CB延长线上一点，直线EA与圆O相切．求证：