题目内容
3.若直线y=kx+2与曲线y=$\sqrt{1-{x^2}}$有两个公共点,则k的取值范围是$[{-2,-\sqrt{3}})∪({\sqrt{3},2}]$.分析 作出直线y=kx+2与曲线y=$\sqrt{1-{x^2}}$的图象,利用数形结合进行求解即可
解答 解:由y=$\sqrt{1-{x^2}}$得x2+y2=1,(y≥0),对应的轨迹为上半圆,
∵直线y=kx+2过定点A(0,2),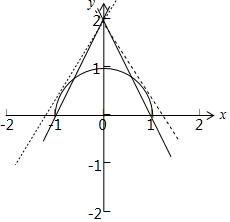
∴当k=±$\sqrt{3}$时,直线y=kx+2与圆x2+y2=1相切,
由图象可知当直线y=kx+2经过点B(-1,0)或C(1,0)时,直线和圆有两个交点,
此时k=±2,
则若直线y=kx+1与曲线y=$\sqrt{1-{x^2}}$恰有两个共同点,
故k∈$[{-2,-\sqrt{3}})∪({\sqrt{3},2}]$
故答案为:$[{-2,-\sqrt{3}})∪({\sqrt{3},2}]$
点评 本题主要考查直线和圆的位置关系的应用,利用数形结合是解决本题的关键

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
14.若△ABC是边长为1的等边三角形,且$\overrightarrow{AD}$=2$\overrightarrow{DB}$,2$\overrightarrow{AE}$=$\overrightarrow{EC}$,则$\overrightarrow{CD}$$•\overrightarrow{BE}$=( )
| A. | -$\frac{1}{9}$ | B. | -$\frac{2}{9}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{7}{18}$ |
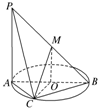 如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M是线段PB的中点.有以下四个命题:
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M是线段PB的中点.有以下四个命题: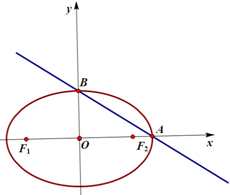 椭圆C;$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别是F1,F2,右顶点为A,上顶点为B,坐标系原点O到直线AB的距离为$\frac{{2\sqrt{21}}}{7}$,椭圆的离心率是$\frac{1}{2}$.
椭圆C;$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别是F1,F2,右顶点为A,上顶点为B,坐标系原点O到直线AB的距离为$\frac{{2\sqrt{21}}}{7}$,椭圆的离心率是$\frac{1}{2}$.