题目内容
2.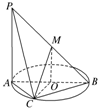 如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M是线段PB的中点.有以下四个命题:
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M是线段PB的中点.有以下四个命题:①MO∥平面PAC;
②PA∥平面MOB;
③OC⊥平面PAC;
④平面PAC⊥平面PBC.
其中正确的命题的序号是①④.
分析 ①先证明MO∥PA,即可判定MO∥平面PAC;
②PA在平面MOB内,可得①错误;
③可证PA⊥BC,BC⊥平面PAC.即可证明OC⊥平面PAC不成立;
④由③知BC⊥平面PAC,即可证明平面PAC⊥平面PBC.
解答  解:①因为MO∥PA,MO?平面PAC,PA?平面PAC,所以MO∥平面PAC;
解:①因为MO∥PA,MO?平面PAC,PA?平面PAC,所以MO∥平面PAC;
②因为PA在平面MOB内,所以①错误;
③因为PA垂直于圆O所在的平面,所以PA⊥BC.
又BC⊥AC,AC∩PA=A,所以BC⊥平面PAC.因为空间内过一点作已知平面的垂线有且只有一条,所以OC⊥平面PAC不成立,③错误;
④由③知BC⊥平面PAC,且BC?平面PBC,所以平面PAC⊥平面PBC.
正确命题的序号是①④.
故答案为:①④.
点评 本题主要考查了直线与平面平行的判定,直线与平面垂直的性质,考查了空间想象能力和推理论证能力,考查了数形结合思想的应用,属于中档题.

练习册系列答案
相关题目
13.已知等差数列{an}的前n项和为Sn,公差为2,且a1,S2,S4成等比数列,则数列{an}的通项公式an等于( )
| A. | 2n+1 | B. | 2n-3 | C. | 2n-1 | D. | 2n |
7.已知函数f(x)=-x3+ax2-x-1在R上不是单调函数,则实数a的取值范围是( )
| A. | [-$\sqrt{3}$,$\sqrt{3}$] | B. | (-$\sqrt{3}$,$\sqrt{3}$) | C. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | D. | (-∞,-$\sqrt{3}$]∪[$\sqrt{3}$,+∞) |