题目内容
9. 如图,已知a∈[2,4],直线l1:a2x+y-4a2-2=0,l2:x+ay-4-2a=0,l1交y轴的正半轴于A,l2交x轴的正半轴于B,l1、l2相交于点C,试求四边形OACB面积的最大值和最小值.
如图,已知a∈[2,4],直线l1:a2x+y-4a2-2=0,l2:x+ay-4-2a=0,l1交y轴的正半轴于A,l2交x轴的正半轴于B,l1、l2相交于点C,试求四边形OACB面积的最大值和最小值.
分析 直线l1:a2x+y-4a2-2=0,即直线l1:a2(x-4)+(y-2)=0,经过定点(4,2).l2:x+ay-4-2a=0,即l2:x-4+a(y-2)=0,经过定点(4,2).可得l1、l2相交于点C(4,2),l1交y轴的正半轴于A(0,4a2+2),l2交x轴的正半轴于B(4+2a,0),a∈[2,4],利用四边形OACB面积S=S△OAC+S△OBC=$\frac{1}{2}|OA|$•xC+$\frac{1}{2}|OB|•{y}_{C}$及其二次函数的单调性即可得出.
解答 解:直线l1:a2x+y-4a2-2=0,即直线l1:a2(x-4)+(y-2)=0,经过定点(4,2).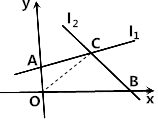
l2:x+ay-4-2a=0,即l2:x-4+a(y-2)=0,经过定点(4,2).
∴l1、l2相交于点C(4,2),
l1交y轴的正半轴于A(0,4a2+2),l2交x轴的正半轴于B(4+2a,0),a∈[2,4],
∴四边形OACB面积S=S△OAC+S△OBC
=$\frac{1}{2}|OA|$•xC+$\frac{1}{2}|OB|•{y}_{C}$
=$\frac{1}{2}$×(4a2+2)×4+$\frac{1}{2}×(4+2a)$×2=8a2+2a+8=8$(a+\frac{1}{8})^{2}$+$\frac{63}{8}$.
∴S在a∈[2,4]单调递增,
a=2时,S=44.a=4时,S=144.
∴S∈[44,144],
其最大值和最小值分别为144,44.
点评 本题考查了直线系的应用、三角形面积计算公式、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.若随机变量ξ的分布列为
其中m∈(0,1),则下列结果中正确的是( )
| ξ | 0 | 1 |
| P | m | n |
| A. | E(ξ)=m,D(ξ)=n3 | B. | E(ξ)=n,D(ξ)=n2 | C. | E(ξ)=1-m,D(ξ)=m-m2 | D. | E(ξ)=1-m,D(ξ)=m2 |
11.某产品的广告费用x万元与销售额y万元的统计数据如下表
根据上表可得回归方程$\widehat{y}$=9x+10.5,则m为( )
| 广告费用x(万元) | 2 | 3 | 4 | 5 |
| 销售额y(万元) | 26 | m | 49 | 54 |
| A. | 36 | B. | 37 | C. | 38 | D. | 39 |
18.已知a1>a2>a3>1,则使得${a_i}{x^2}+(a_i^2+1)x+{a_i}>0$(i=1,2,3)都成立的x的取值范围是( )
| A. | $(0,\frac{1}{a_3})$ | B. | $(-∞,-{a_3})∪(-\frac{1}{a_3},+∞)$ | ||
| C. | $(-∞,-{a_3}]∪(-\frac{1}{a_3},+∞)$ | D. | $(-∞,-\frac{1}{a_3})∪(-{a_3},+∞)$ |
 如图,已知四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,
如图,已知四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,