题目内容
已知函数f(x)=x+
,
(1)判断f(x)在区间(1,+∞)上的单调性,并用定义证明;
(2)当x∈(-∞,0)时,写出函数f(x)=x+
的单调区间(不必证明).
| 1 |
| x |
(1)判断f(x)在区间(1,+∞)上的单调性,并用定义证明;
(2)当x∈(-∞,0)时,写出函数f(x)=x+
| 1 |
| x |
考点:利用导数研究函数的单调性,函数的单调性及单调区间
专题:导数的概念及应用
分析:(1)用定义证明函数的单调性,先设给定区间内任意两个自变量x1,x2,设出x1,x2的大小关系,再计算f( x1)-f( x2),作差后,把差化简为几个因式的乘积的形式,比较每个因式与0的大小,就可得到f( x1)与f( x2)的大小关系,进而根据函数单调性的定义判断函数的单调性.
(2)利用导数求出函数的单调区间即可.
(2)利用导数求出函数的单调区间即可.
解答:
解:(1)f(x)在区间(1,+∞)上的单调递减,
设x1,x2∈(1,+∞),且设x1<x2,
则f(x1)-f(x2)=x1+
-x2-
=
,
∵x1<x2,
∴x1-x2<0,x1•x2>1,
∴f(x1)-f(x2)<0,
∴f(x)在区间(1,+∞)上的单调递减.
(2)∵f(x)=x+
,
∴f′(x)=1-
=
,
令f′(x)=0,
解得x=1或x=-1,
∴函数f(x)在(-∞,-1)上单调递增,在(-1,0)上单调递减
设x1,x2∈(1,+∞),且设x1<x2,
则f(x1)-f(x2)=x1+
| 1 |
| x1 |
| 1 |
| x2 |
| (x1-x2)(x1x2-1) |
| x1x2 |
∵x1<x2,
∴x1-x2<0,x1•x2>1,
∴f(x1)-f(x2)<0,
∴f(x)在区间(1,+∞)上的单调递减.
(2)∵f(x)=x+
| 1 |
| x |
∴f′(x)=1-
| 1 |
| x2 |
| x2-1 |
| x2 |
令f′(x)=0,
解得x=1或x=-1,
∴函数f(x)在(-∞,-1)上单调递增,在(-1,0)上单调递减
点评:本题主要考查了函数的单调性的定义证明和利用导数求函数的单调区间,属于基础题.

练习册系列答案
相关题目
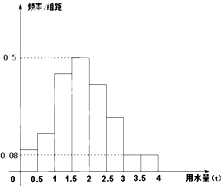 为了解某社区家庭的月均用水量(单位:吨),现从该社区随机抽查100户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图).
为了解某社区家庭的月均用水量(单位:吨),现从该社区随机抽查100户,获得每户某年的月均用水量,并制作了频率分布表和频率分布直方图(如图).