题目内容
如图，直三棱柱ABC-A1B1C1中，点D是BC上一点．（1）若点D是BC的中点，求证：A1C∥平面AB1D；
（2）若平面AB1D⊥平面BCC1B1，求证：AD⊥BC．
考点：直线与平面垂直的性质,直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）利用三角形中位线的性质证明线线平行，再根据直线与平面平行的判定定理即可证明A1C∥平面AB1D．
（2）首先根据直线与平面垂直的判定定理证明AD⊥平面BCC1B1，再利用直线与平面垂直的性质可得AD⊥BC．
（2）首先根据直线与平面垂直的判定定理证明AD⊥平面BCC1B1，再利用直线与平面垂直的性质可得AD⊥BC．
解答：
证明：
（1）连接A1B，设AB1∩A1B=E，
则E为A1B 的中点，
连接DE，由D是BC的中点，
可得DE是△A1BC的中位线．
∴DE∥A1C，
又DE?平面AB1D，且A1C?平面AB1D，
所以A1C∥平面AB1D．
（2）在平面BCC1B1中过点B作BF⊥B1D，
∵平面AB1D⊥平面BCC1B1，
平面AB1D∩平面BCC1B1=B1D，
∴BF⊥平面AB1D，
又∵AD?平面AB1D
∴BF⊥AD，
在直三棱柱ABC-A1B1C1中，
BB1⊥平面ABC，
∴BB1⊥AD，
又BB1∩BF=B，
∴AD⊥平面BCC1B1，
又∵BC?平面BCC1B1
∴AD⊥BC．
（1）连接A1B，设AB1∩A1B=E，则E为A1B 的中点，
连接DE，由D是BC的中点，
可得DE是△A1BC的中位线．
∴DE∥A1C，
又DE?平面AB1D，且A1C?平面AB1D，
所以A1C∥平面AB1D．
（2）在平面BCC1B1中过点B作BF⊥B1D，
∵平面AB1D⊥平面BCC1B1，
平面AB1D∩平面BCC1B1=B1D，
∴BF⊥平面AB1D，
又∵AD?平面AB1D
∴BF⊥AD，
在直三棱柱ABC-A1B1C1中，
BB1⊥平面ABC，
∴BB1⊥AD，
又BB1∩BF=B，
∴AD⊥平面BCC1B1，
又∵BC?平面BCC1B1
∴AD⊥BC．
点评：本题考查直线与平面平行的判定定理，直线与平面垂直的判定定理，以及直线与平面垂直的性质等知识的综合运用．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
相关题目
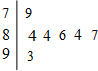如图是2013年某大学自主招生面试环节中，七位评委为某考生打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和众数依次为（ ）| A、85，84 |
| B、84，85 |
| C、86，84 |
| D、84，86 |
在2010年的人口普查中，某市人中普查办公室为召开普查工作意见反馈会，用分层抽样的方法，从某住宅小区中抽取A、B、C、D四个年龄段的居民共50人．如图是该小区这四个年龄段的人数条形图．
