题目内容
讨论函数f(x)=ax2-x-1的零点个数.
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:根据函数的解析式以及函数零点的定义,分类讨论求得函数的零点个数.
解答:
解:对于函数f(x)=ax2-x-1,当a=0时,f(x)=-x-1有唯一零点x=-1.
当a≠0时,由于判别式△=1+4a,若a<-
,则△<0,二次函数f(x)无零点;
若a>-
,且a≠0,则△>0,二次函数f(x)有2个不同的零点;
若a=-
,则△=0,二次函数f(x)有唯一零点.
综上可得,当a=0或a=-
时,函数f(x)有唯一零点;当a<-
,函数f(x)无零点;当a>-
,且a≠0 时,f(x)有2个不同的零点.
当a≠0时,由于判别式△=1+4a,若a<-
| 1 |
| 4 |
若a>-
| 1 |
| 4 |
若a=-
| 1 |
| 4 |
综上可得,当a=0或a=-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
点评:本题主要考查函数零点的定义,二次函数的性质,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
已知A={2,lnx},B={x,y},A∩B={1},则实数x,y的值分别为( )
| A、e,0 | ||
| B、e,1 | ||
| C、1,e | ||
D、
|
设动点A、B均在双曲线C:
-
=1(a>0,b>0)的右支上,点O为坐标原点,双曲线C的离心率为e,则( )
| x2 |
| a2 |
| y2 |
| b2 |
A、若e>
| ||||||
B、若1≤e≤
| ||||||
C、若e>
| ||||||
D、若1<e≤
|
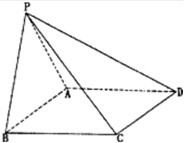 如图所示,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,平面PAB⊥平面ABCD,PA=PB=AB.
如图所示,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,平面PAB⊥平面ABCD,PA=PB=AB.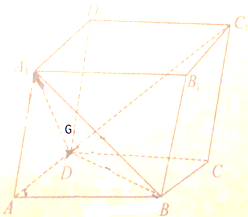 如图,在平行六面体ABCD-A1B1C1D1中,G为△A1BD的重心,设
如图,在平行六面体ABCD-A1B1C1D1中,G为△A1BD的重心,设