题目内容
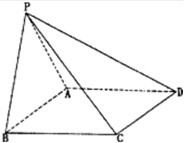 如图所示,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,平面PAB⊥平面ABCD,PA=PB=AB.
如图所示,四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,平面PAB⊥平面ABCD,PA=PB=AB.(1)证明:PC⊥AB;
(2)求二面角B-PC-D的余弦值.
考点:二面角的平面角及求法,直线与平面垂直的性质
专题:空间位置关系与距离,空间角
分析:(1)取AB中点O,连结PO,CO,由已知条件推导出AB⊥平面POC,由此能证明PC⊥AB.
(2)以O为原点,OB为x轴,OC为y轴,OP为z轴,建立空间直角坐标系,利用向量法能求出二面角B-PC-D的余弦值.
(2)以O为原点,OB为x轴,OC为y轴,OP为z轴,建立空间直角坐标系,利用向量法能求出二面角B-PC-D的余弦值.
解答:
 (1)证明:取AB中点O,连结PO,CO,
(1)证明:取AB中点O,连结PO,CO,
∵四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,
PA=PB=AB.
∴PO⊥AB,CO⊥AB,
∵PO∩CO=O,
∴AB⊥平面POC,
∵PC∈平面POC,∴PC⊥AB.
(2)解:∵平面PAB⊥平面ABCD,CO⊥AB,PO⊥AB,
∴以O为原点,OB为x轴,OC为y轴,OP为z轴,
建立空间直角坐标系,
设PA=PB=AB=2,则B(1,0,0),P(0,0,
),
C(0,
,0),D(-2,
,0),
=(1,0,-
),
=(0,
,-
),
=(-2,
,-
),
设平面BPC的法向量
=(x,y,z),
则
,取x=
,得
=(
,1,1),
设平面PCD的法向量
=(a,b,c),
则
,取b=1,得
=(0,1,1),
设二面角B-PC-D的平面角为θ,
cosθ=|cos<
,
>|=|
|=
.
∴二面角B-PC-D的余弦值为
.
 (1)证明:取AB中点O,连结PO,CO,
(1)证明:取AB中点O,连结PO,CO,∵四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,
PA=PB=AB.
∴PO⊥AB,CO⊥AB,
∵PO∩CO=O,
∴AB⊥平面POC,
∵PC∈平面POC,∴PC⊥AB.
(2)解:∵平面PAB⊥平面ABCD,CO⊥AB,PO⊥AB,
∴以O为原点,OB为x轴,OC为y轴,OP为z轴,
建立空间直角坐标系,
设PA=PB=AB=2,则B(1,0,0),P(0,0,
| 3 |
C(0,
| 3 |
| 3 |
| PB |
| 3 |
| PC |
| 3 |
| 3 |
| PD |
| 3 |
| 3 |
设平面BPC的法向量
| n |
则
|
| 3 |
| n |
| 3 |
设平面PCD的法向量
| m |
则
|
| m |
设二面角B-PC-D的平面角为θ,
cosθ=|cos<
| n |
| m |
| 0+1+1 | ||||
|
| ||
| 5 |
∴二面角B-PC-D的余弦值为
| ||
| 5 |
点评:本题考查异面直线垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
命题:“?x∈R,x2-x+2<0”的否定是( )
| A、?x∈R,x2-x+2≥0 |
| B、?x∈R,x2-x+2≥0 |
| C、?x∈R,x2-x+2<0 |
| D、?x∈R,x2-x+2<0 |
在集合{a,b,c,d}上定义两种运算⊕和?如下:

那么d?(a⊕c)=( )

那么d?(a⊕c)=( )
| A、a | B、b | C、c | D、d |
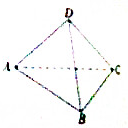 在空间四边形ABCD中,各边长均为a,对角线BD=
在空间四边形ABCD中,各边长均为a,对角线BD=