题目内容
已知函数f(x)=
,x∈(-1,1)
(Ⅰ)若x∈(0,1)试判断此时函数f(x)的单调性并利用定义证明;
(Ⅱ)若设g(x)=f(x)+f(-x),求函数g(x)的值域.
| 2x |
| 4x+1 |
(Ⅰ)若x∈(0,1)试判断此时函数f(x)的单调性并利用定义证明;
(Ⅱ)若设g(x)=f(x)+f(-x),求函数g(x)的值域.
考点:函数单调性的判断与证明,函数的值域
专题:函数的性质及应用
分析:(Ⅰ)首先,得到f(x)为(-1,1)上的减函数,然后,结合单调性的定义进行证明;
(Ⅱ)首先,落实函数g(x)的表达式,然后,结合基本不等式求解其值域即可.
(Ⅱ)首先,落实函数g(x)的表达式,然后,结合基本不等式求解其值域即可.
解答:
解:(Ⅰ)f(x)为(-1,1)上的减函数,证明如下:
任意设x1,x2∈(-1,1)x1<x2,
∴f(x1)-f(x2)=
-
=
,
∵x1<x2,
∴2x2-2x1>0,
∴f(x1)-f(x2)>0,
∴f(x1)>f(x2),
∴f(x)为(-1,1)上的减函数.
(Ⅱ)∵g(x)=f(x)+f(-x),
∴g(x)=
+
,
=2
,
=
,
∵2x+
≥2,
∴0<f(x)≤1,
∴值域为(0,1].
任意设x1,x2∈(-1,1)x1<x2,
∴f(x1)-f(x2)=
| 2x1 |
| 4x1+1 |
| 2x2 |
| 4x2+1 |
=
| (2x2-2x1)(1+2x1+x2) |
| (4x1+1)(4x2+1) |
∵x1<x2,
∴2x2-2x1>0,
∴f(x1)-f(x2)>0,
∴f(x1)>f(x2),
∴f(x)为(-1,1)上的减函数.
(Ⅱ)∵g(x)=f(x)+f(-x),
∴g(x)=
| 2x |
| 4x+1 |
| 2x |
| 4x+1 |
=2
| 2x |
| 4x+1 |
=
| 2 | ||
2x+
|
∵2x+
| 1 |
| 2x |
∴0<f(x)≤1,
∴值域为(0,1].
点评:本题重点考查了指数函数的单调性和基本性质、函数的单调性的定义的证明过程等知识,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
将边长为1的正方形ABCD沿对角线BD折成直二面角,若点P满足
=
-
+
,则|
|的值为( )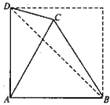
| BP |
| 1 |
| 2 |
| BA |
| 1 |
| 2 |
| BC |
| BD |
| BP |

A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
双曲线的一个焦点F(4,0)到渐近线的距离为2,则双曲线的离心率是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知f(x)是奇函数,且f(x+2)=f(x),当0≤x≤1时,f(x)=2x(1-x),则f(-
)=( )
| 5 |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|