题目内容
10.某三棱锥的三视图如图所示,则该三棱锥的表面积为( )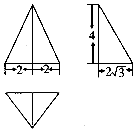
| A. | $4\sqrt{3}+8+2\sqrt{19}$ | B. | $4\sqrt{3}+8+4\sqrt{19}$ | C. | $8\sqrt{3}+8+4\sqrt{19}$ | D. | $8\sqrt{3}+8+2\sqrt{19}$ |
分析 由三视图可知该三棱锥底面是边长为4的正三角形,两个侧面是全等的三角形,三边分别为2$\sqrt{5}$,2$\sqrt{7}$,4,另一个侧面为等腰三角形,求出各个侧面面积即可得到表面积.
解答 解:由三视图可知该三棱锥底面是边长为4的正三角形,面积为4$\sqrt{3}$,两个侧面是全等的三角形,三边分别为2$\sqrt{5}$,2$\sqrt{7}$,4,面积之和为4$\sqrt{19}$,另一个侧面为等腰三角形,面积是$\frac{1}{2}$×4×4=8,
故选B.
点评 本题考查了由三视图求几何体的表面积,解题的关键是由三视图判断几何体的形状及数据所对应的几何量.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.函数f(x)在(0,+∞)上为增函数,则不等式f(x)>f(8x-16)的解集为( )
| A. | (2,$\frac{16}{7}$) | B. | (-∞,2) | C. | ($\frac{16}{7}$,+∞) | D. | (2,+∞) |
19.已知f(x)=$\left\{\begin{array}{l}{2x+3,x<0}\\{2{x}^{2}+1,x≥0}\end{array}\right.$,则f[f(-1)]的值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
20.已知tan(α+$\frac{π}{4}$)=$\frac{1}{2}$,且α∈(-$\frac{π}{2}$,0),则$\frac{{2{{sin}^2}α+sin2α}}{{cos(α-\frac{π}{4})}}$=( )
| A. | $-\frac{{3\sqrt{5}}}{10}$ | B. | $-\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{3\sqrt{10}}}{10}$ |