题目内容
2.已知函数f(x)=$\frac{x+a}{3x-2}$,x∈[1,4],且f(1)=2.(1)求函数的解析式并证明函数的单调性;
(2)求函数y=f(x)的最大值和最小值.
分析 (1)将由f(1)=-1求出a=1,代入f(x),求出函数的解析式,里用定义法证明函数的单调性;
(2)根据函数单调性的求出最值即可.
解答 证明:(1)$f(1)=\frac{1+a}{3-2}=2$,∴a=1,
∴函数的解析式:f(x)=$\frac{x+1}{3x-2}$,x∈[1,4]
设任取x1,x2∈[1,4],且x1<x2,
f(x1)-f(x2)=$\frac{{x}_{1}+1}{3{x}_{1}-2}-\frac{{x}_{2}+1}{3{x}_{2}-2}$=$\frac{5({x}_{2}-{x}_{1})}{(3{x}_{1}-2)(3{x}_{2}-2)}$
∵1≤x1<x2≤4,x1-x2<0,3(x1-2)>0,3(x2-2)>0
∴f(x1)-f(x2)>0,即f(x1)>f(x2),
∴f(x)在[1,4]上为减函数.
解:(2)由(1)知,f(x)在[1,4]上为减函数,
f(x)max=f(1)=2,$f{(x)_{min}}=f(4)=\frac{1}{2}$.
点评 本题考查了用定义法证明函数的单调性,及函数的最值,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
13.已知函数f(x)=$\left\{\begin{array}{l}{-x,x≤0}\\{{x}^{2}+2,x>0}\end{array}\right.$,则f(f(-1))的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.某三棱锥的三视图如图所示,则该三棱锥的表面积为( )
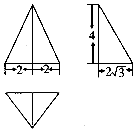
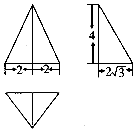
| A. | $4\sqrt{3}+8+2\sqrt{19}$ | B. | $4\sqrt{3}+8+4\sqrt{19}$ | C. | $8\sqrt{3}+8+4\sqrt{19}$ | D. | $8\sqrt{3}+8+2\sqrt{19}$ |
7.已知a=0.21.5,b=20.1,c=0.21.3,则a,b,c的大小关系是( )
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | b<c<a |
12.已知函数f(x)=$\frac{2{x}^{2}-1}{{x}^{2}+2}$,则函数f(x)的值域是( )
| A. | [-$\frac{1}{2}$,1] | B. | [-$\frac{1}{2}$,2] | C. | [-$\frac{1}{2}$,2) | D. | (-$\frac{1}{2}$,1) |
 已知函数f(x)=x2-2|x|.
已知函数f(x)=x2-2|x|.