题目内容
18.关于下列命题:①若函数y=2x+1的定义域是{x|x≤0},则它的值域是{y|y≤1};
②若函数y=$\frac{1}{x}$的定义域是{x|x>2},则它的值域是{y|y≤$\frac{1}{2}$};
③若函数y=x2的值域是{y|0≤y≤4},则它的定义域一定是{x|-2≤x≤2};
④若函数y=x+$\frac{1}{x}$的定义域是{x|x<0},则它的值域是{y|y≤-2}.
其中不正确的命题的序号是②③.(注:把你认为不正确的命题的序号都填上)
分析 逐项分析.①根据一次函数的单调性易得;②根据反比例函数的图象和性质易知其值域应为(0,$\frac{1}{2}$);③可举反例说明;④利用均值不等式可得.
解答 解:①当x≤0时,2x+1≤1,故①正确;
②由反比例函数的图象和性质知,当x>2时,$0<\frac{1}{x}<\frac{1}{2}$,故②错误;
③当函数定义域为[0,2]时,函数值域也为[0,4],故③错误;
④当x<0时,$y=x+\frac{1}{x}=-[(-x)+\frac{1}{-x}]$.因为$(-x)+\frac{1}{-x}≥2\sqrt{(-x)•\frac{1}{-x}}=2$,所以y≤-2,故④正确.
综上可知:②③错误.
故答案为:②③.
点评 本题考查函数的概念和性质.利用函数性质和图象是解题关键.其中命题④的判断是本题易错点.属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
9.设集合A={y|y=log2x,x>1},B={y|y=($\frac{1}{2}$)x,0<x<1},则A∩B等于( )
| A. | {y|$\frac{1}{2}$<y<1} | B. | {y|0<y$<\frac{1}{2}$} | C. | ∅ | D. | {y|0<y<1} |
6.对于天气预报说“明天降水的概率为80%”的正确解释是( )
| A. | 明天上午下雨,下午不下雨 | |
| B. | 明天下雨的概率为80% | |
| C. | 明天有的地方下雨,有的地方不下雨 | |
| D. | 明天下雨的时间一共是19.2小时 |
13.已知函数f(x)=$\left\{\begin{array}{l}{-x,x≤0}\\{{x}^{2}+2,x>0}\end{array}\right.$,则f(f(-1))的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.某三棱锥的三视图如图所示,则该三棱锥的表面积为( )
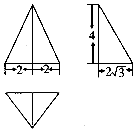
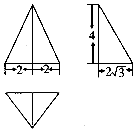
| A. | $4\sqrt{3}+8+2\sqrt{19}$ | B. | $4\sqrt{3}+8+4\sqrt{19}$ | C. | $8\sqrt{3}+8+4\sqrt{19}$ | D. | $8\sqrt{3}+8+2\sqrt{19}$ |
7.已知a=0.21.5,b=20.1,c=0.21.3,则a,b,c的大小关系是( )
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | b<c<a |