题目内容
20.在上海世界博览会开展期间,计划选派部分高二学生参加宣传活动,报名参加的学生需进行测试,共设4道选择题,规定必须答完所有题,且答对一题得1分,答错一题扣1分,至少得2分才能入选成为宣传员;甲乙丙三名同学报名参加测试,他们答对每个题的概率都为$\frac{1}{3}$,且每个人答题相互不受影响.(1)用随机变量ξ表示能够成为宣传员的人数,求ξ的数学期望与方差;
(2)若学生甲得分的数值为随机变量η,求所得分数η的分布列和数学期望.
分析 (1)每个同学通过测试需得(2分)或(4分),即答对3道或4道试题.利用二项分布概率计算公式即可得出概率.由每个人答题相互不受影响,可得三人是否成为宣传员是相互独立事件,又因为每个人成为宣传员的概率均为$\frac{1}{9}$,故为独立重复试验,又随机变量ξ表示能够成为宣传员的人数,即3次独立重复试验中发生ξ次的概率,因此随即变量ξ满足二项分布,ξ~B$(3,\frac{1}{9})$.
(2)所得分数η的所有取值为-4,-2,0,2,4.利用二项分布列即可得出.
解答 解:(1)每个同学通过测试需得(2分)或(4分),即答对3道或4道试题.
所以$P=C_4^3{(\frac{1}{3})^3}×(1-\frac{1}{3})+{(\frac{1}{3})^4}=\frac{1}{9}$;
∵每个人答题相互不受影响,∴三人是否成为宣传员是相互独立事件,又因为每个人成为宣传员的概率均为$\frac{1}{9}$,故为独立重复试验,又随机变量ξ表示能够成为宣传员的人数,即3次独立重复试验中发生ξ次的概率,∴随即变量ξ满足二项分布,$ξ\~B(3,\frac{1}{9})$,
∴$Eξ=3×\frac{1}{9}=\frac{1}{3},Dξ=3×\frac{1}{9}×(1-\frac{1}{9})=\frac{8}{27}$.
(2)所得分数η的所有取值为-4,-2,0,2,4.
$P(ξ=-4)={(1-\frac{1}{3})^4}=\frac{16}{81}$,$P(ξ=-2)=C_4^1×\frac{1}{3}×{(1-\frac{1}{3})^3}=\frac{32}{81}$,$P(ξ=0)=C_4^2×{(\frac{1}{3})^2}×{(1-\frac{1}{3})^2}=\frac{24}{81}=\frac{8}{27}$,$P(ξ=2)=C_4^3×{(\frac{1}{3})^3}×{(1-\frac{1}{3})^{\;}}=\frac{8}{81}$,$P(ξ=4)={(\frac{1}{3})^4}=\frac{1}{81}$.
| η | -4 | -2 | 0 | 2 | 4 |
| P | $\frac{16}{81}$ | $\frac{32}{81}$ | $\frac{8}{27}$ | $\frac{8}{81}$ | $\frac{1}{81}$ |
点评 本题考查了二项分布列的概率计算与数学期望,考查了推理能力与计算能力,属于中档题.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | {y|$\frac{1}{2}$<y<1} | B. | {y|0<y$<\frac{1}{2}$} | C. | ∅ | D. | {y|0<y<1} |
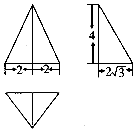
| A. | $4\sqrt{3}+8+2\sqrt{19}$ | B. | $4\sqrt{3}+8+4\sqrt{19}$ | C. | $8\sqrt{3}+8+4\sqrt{19}$ | D. | $8\sqrt{3}+8+2\sqrt{19}$ |