题目内容
下列函数中,不具有奇偶性的函数是( )
| A、y=ex-e-x | ||
B、y=lg
| ||
| C、y=cos2x | ||
| D、y=sinx+cosx |
考点:余弦函数的奇偶性
专题:函数的性质及应用
分析:根据函数奇偶性的定义进行判断即可.
解答:
解:A.f(-x)=e-x-ex=-(ex-e-x)=-f(x),则函数是y=ex-e-x奇函数,
B.f(-x)=lg
=lg(
)-1=-lg
=-f(x),则函数f(x)是奇函数,
C.y=cos2x为偶函数,
D.f(-x)=-sinx+cosx,则f(-x)≠f(x),且f(-x)≠-f(x),则f(x)既不是奇函数也不是偶函数,不具备奇偶性,
故选:D
B.f(-x)=lg
| 1-x |
| 1+x |
| 1+x |
| 1-x |
| 1+x |
| 1-x |
C.y=cos2x为偶函数,
D.f(-x)=-sinx+cosx,则f(-x)≠f(x),且f(-x)≠-f(x),则f(x)既不是奇函数也不是偶函数,不具备奇偶性,
故选:D
点评:本题主要考查函数奇偶性的判断,根据函数奇偶性的定义是解决本题的关键.

练习册系列答案
相关题目
用秦九韶算法计算多项式f(x)=2x5-3x4+7x3-9x2+4x-10在x=2时的值时,V3的值为( )
| A、34 | B、22 | C、9 | D、1 |
计算:[(-
)2]-1=( )
| 2 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
若m,n是正整数,则m+n>mn成立的充要条件是( )
| A、m,n都等于1 |
| B、m,n都不等于2 |
| C、m,n都大于1 |
| D、m,n至少有一个等于1 |
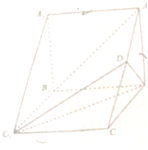 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点,AA1=AB=2.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,△ABC是等边三角形,D为AC的中点,AA1=AB=2.