题目内容
 如图,把边长为10的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖六棱柱盒子,设其高为h,体积为V(不计接缝).
如图,把边长为10的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖六棱柱盒子,设其高为h,体积为V(不计接缝).(Ⅰ)求出体积V与高h的函数关系式并指出其定义域;
(Ⅱ)问当h为多少时,体积V最大?最大值是多少?
考点:基本不等式在最值问题中的应用,基本不等式
专题:应用题,导数的综合应用,不等式的解法及应用
分析:(Ⅰ)求出六棱柱的底边长、底面积,可得体积V与高h的函数关系式;
(Ⅱ)利用导数法,可求最大值.
(Ⅱ)利用导数法,可求最大值.
解答:
解:(Ⅰ)由题意知,六棱柱的底边长为10-
h,(1分)
底面积为6•
(10-
h)2(3分)
由10-
h>0及h>0得0<h<5
∴体积V=
(10-
h)2•h=2
(h3-10
h2+75h),
其定义域为(0,5
)(6分)
(Ⅱ)由V′=2
(3h2-20
h+75)=0
得h=
或h=5
(舍去) (8分)
∵0<h<
时,V′>0;
<h<5
时,V′<0.(10分)
∴当h=
时V有最大值
.(12分)
2
| ||
| 3 |
底面积为6•
| ||
| 4 |
2
| ||
| 3 |
由10-
2
| ||
| 3 |
| 3 |
∴体积V=
3
| ||
| 2 |
2
| ||
| 3 |
| 3 |
| 3 |
其定义域为(0,5
| 3 |
(Ⅱ)由V′=2
| 3 |
| 3 |
得h=
5
| ||
| 3 |
| 3 |
∵0<h<
5
| ||
| 3 |
5
| ||
| 3 |
| 3 |
∴当h=
5
| ||
| 3 |
| 1000 |
| 3 |
点评:本题考查体积的计算,考查利用数学知识解决实际问题,正确运用导数法是关键.

练习册系列答案
相关题目
将函数f(x)=sin(2x+φ)(0<φ<π)的图象上所有点向右平移
个单位后得到的图象关于原点对称,则φ等于( )
| π |
| 6 |
| A、0 | ||
B、
| ||
C、
| ||
D、
|
程序框图(如图)的运算结果为( )


| A、2 | B、6 | C、18 | D、24 |
已知a>0且a≠1,则在下面所给出的四种图形中,正确表示函数y=ax和y=logax的图象一定是( )

| A、①③ | B、②③ | C、②④ | D、①④ |
已知复数z1=2+i,z2=a-3i(i为虚数单位,a∈R).若z1•z2为实数,则a的值为( )
| A、3 | B、4 | C、5 | D、6 |
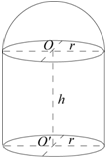 要设计一个金属容积为V(常数)的密闭容器,下部是圆柱形,上部为半球形(如图).当圆柱底面半径r与高h各为何值时,制造这个容器用料最省(表面积最小)?
要设计一个金属容积为V(常数)的密闭容器,下部是圆柱形,上部为半球形(如图).当圆柱底面半径r与高h各为何值时,制造这个容器用料最省(表面积最小)?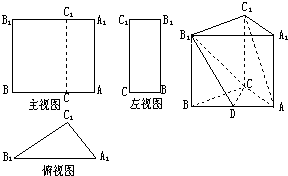 已知三棱柱ABC-A1B1C1的三视图与直观图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5,B1C1=4,
已知三棱柱ABC-A1B1C1的三视图与直观图如图所示,其中主视图AA1B1B和左视图B1BCC1均为矩形,在俯视图△A1B1C1中,A1C1=3,A1B1=5,B1C1=4,