题目内容
设数列{an}的前n项和为sn,满足点(n,sn)在函数f(x)=x2-8x图象上,{bn}为等比数列,且b1=a5,b2+a3=-1
(1)求数列{an}和{bn}的通项公式;
(2)设cn=anbn,求数列的前项n和Tn.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=anbn,求数列的前项n和Tn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由点(n,sn)在函数f(x)=x2-8x的图象上得到数列递推式Sn=n2-8n,由an=sn-sn-1=求得数列的通项公式.再由数列{bn}为等比数列,b1=a5=1,b2=2求得公比,代入等比数列的通项公式求得bn;
(2)把an=2n-9,bn=2n-1代入cn=anbn,然后由错位相减法求得数列的前项n和Tn.
(2)把an=2n-9,bn=2n-1代入cn=anbn,然后由错位相减法求得数列的前项n和Tn.
解答:
解:(1)∵点(n,sn)在函数f(x)=x2-8x的图象上,
∴Sn=n2-8n,
当n=1时,a1=s1=-7,
当n≥2时,an=sn-sn-1=(n2-8n)-[(n-1)2-8(n-1)]=2n-9,
而a1=-7满足上式,
∴an=2n-9.
∵数列{bn}为等比数列,b1=a5=1,b2=2,
∴q=2,则bn=2n-1;
(2)由(1)知an=2n-9,bn=2n-1,
则Cn=(2n-9)•2n-1,
则Tn=(-7)×20+(-5)×2+(-3)×22+…+(2n-11)•2n-2+(2n-9)•2n-1 ①,
2Tn=(-7)×2+(-5)×22+…+(2n-13)•2n-2+(2n-11)•2n-1+(2n-9)•2n ②,
①-②得,
-Tn=-7+2(2+22+23+…+2n-1)-(2n-9)•2n
=-7+2×
-(2n-9)•2n=(11-2n)•2n-11.
∴Tn=(2n-11)•2n+11.
∴Sn=n2-8n,
当n=1时,a1=s1=-7,
当n≥2时,an=sn-sn-1=(n2-8n)-[(n-1)2-8(n-1)]=2n-9,
而a1=-7满足上式,
∴an=2n-9.
∵数列{bn}为等比数列,b1=a5=1,b2=2,
∴q=2,则bn=2n-1;
(2)由(1)知an=2n-9,bn=2n-1,
则Cn=(2n-9)•2n-1,
则Tn=(-7)×20+(-5)×2+(-3)×22+…+(2n-11)•2n-2+(2n-9)•2n-1 ①,
2Tn=(-7)×2+(-5)×22+…+(2n-13)•2n-2+(2n-11)•2n-1+(2n-9)•2n ②,
①-②得,
-Tn=-7+2(2+22+23+…+2n-1)-(2n-9)•2n
=-7+2×
| 2(1-2n-1) |
| 1-2 |
∴Tn=(2n-11)•2n+11.
点评:本题考查了数列递推式,考查了错位相减法求数列的和,是中档题.

练习册系列答案
相关题目
“
>0”是“x>l”的( )
| x-1 |
| x |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
执行如图所示的程序框图,输出的S值为( )


| A、7 | B、8 | C、16 | D、24 |
把函数y=sin(2x+
)的图象上各点的横坐标缩短为原来的
,纵坐标不变,所得的函数解析式为( )
| π |
| 6 |
| 1 |
| 2 |
A、y=sin(4x+
| ||
B、y=sin(4x+
| ||
C、y=sin(x+
| ||
D、y=sin(x+
|
数列{an}:2,5,11,20,m,47…猜想{an}中的m等于( )
| A、27 | B、28 | C、31 | D、32 |
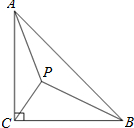 如图所示,△ABC为直角三角形,CA=
如图所示,△ABC为直角三角形,CA=