��Ŀ����
��֪����f��x��=
��x��0����g��x��=sinx-ax��x��0����
������f��x��=
��x��0��������С�������У���Ϊ����{xn}����{xn}��ǰn���Sn��
������f��x����g��x����x�ʣ�0��+�ޣ��Ϻ��������ʵ��a��ȡֵ��Χ��
�������P�Ǻ����գ�x����أ�x��ͼ��Ľ��㣬��ֱ��lͬʱ�뺯���գ�x�����أ�x����ͼ��������P�㣬�Һ����գ�x�����أ�x����ͼ��λ��ֱ��l�����࣬���ֱ��lΪ�����գ�x�����أ�x���ķ����ߣ�
̽�����Ƿ����ʵ��a��ʹ�ú���f��x����g��x�����ڷ����ߣ������ڣ����ʵ��a��ֵ����д�������߷��̣��������ڣ���˵�����ɣ�
| cosx |
| x |
������f��x��=
| cosx |
| x |
������f��x����g��x����x�ʣ�0��+�ޣ��Ϻ��������ʵ��a��ȡֵ��Χ��
�������P�Ǻ����գ�x����أ�x��ͼ��Ľ��㣬��ֱ��lͬʱ�뺯���գ�x�����أ�x����ͼ��������P�㣬�Һ����գ�x�����أ�x����ͼ��λ��ֱ��l�����࣬���ֱ��lΪ�����գ�x�����أ�x���ķ����ߣ�
̽�����Ƿ����ʵ��a��ʹ�ú���f��x����g��x�����ڷ����ߣ������ڣ����ʵ��a��ֵ����д�������߷��̣��������ڣ���˵�����ɣ�
���㣺�����뺯�����ۺ�,���õ����о������ĵ�����
ר�⣺�������ۺ�Ӧ��,�Ȳ�������ȱ�����
�����������ݺ������Ķ����
=0����x�ķ�Χ�����Һ���������ֵ���жϳ�����{xn}�ǵȲ����У�����Ȳ����е�ͨ�ʽ���Sn��
������f��x����g��x�����������a���ٹ��캯����(x)=
����������жϳ���������������ļ���ֵ�����ֵ�������a�ķ�Χ��
�����������ã���f��x����g��x������f��x����g��x�����ڣ�0��+�ޣ��Ϻ���������ݼ���˼������ų����ٸ���a�ķ�Χ�������ͼ��Ľ������꣬������߷��̺����õ������ֱ��жϳ�����f��x����g��x����ͼ�������ߵ�λ�ù�ϵ��
| cosx |
| x |
������f��x����g��x�����������a���ٹ��캯����(x)=
| xsinx-cosx |
| x2 |
�����������ã���f��x����g��x������f��x����g��x�����ڣ�0��+�ޣ��Ϻ���������ݼ���˼������ų����ٸ���a�ķ�Χ�������ͼ��Ľ������꣬������߷��̺����õ������ֱ��жϳ�����f��x����g��x����ͼ�������ߵ�λ�ù�ϵ��
���
�⣺����������ã�
=0��x��0������cosx=0��
��x=
+k����xn=
+(n-1)����
������{xn}���Ԧ�Ϊ�����
Ϊ����ĵȲ����У�
��Sn=
+
=
��
����f��x����g��x����x�ʣ�0��+�ޣ��Ϻ������
��
��sinx-ax����a��
��
����(x)=
��
���ա�(x)=
=
��x��0��x2+2��0��
��գ�x��������(0��
)�ϵ���������������(
��
)�ϵ����ݼ���
������(
+2k�У�
+2k��)(k��z)�ϵ����ݼ���
������(
+2k�У�
+2k��)(k��z)�ϵ���������
��գ�x���ļ���ֵΪ��(
+2k��)=
(k��N)��
�ʦգ�x�������ֵΪ��(
)=
��
����a��
��
����������f��x����g��x�����ڷ����ߣ����С�f��x����g��x������f��x����g��x����
�ڣ�0��+�ޣ��Ϻ������
��x��0ʱ��f��x��=
��+�ޣ�g��x��=sinx-ax��0��
��?x0�ʣ�0��?��ʹ��f��x����g��x������f��x����g��x���ڣ�0��+�ޣ��ϲ��������
��ֻ����f��x����g��x���ڣ�0��+�ޣ��Ϻ������
�ɣ��ã�a��
���ߺ���f��x����g��x��������ڽ��㣬
��a=
��
��a=
ʱ������f��x����g��x���Ľ���Ϊ��(
��0)��
��f��(
)=-
=g��(
)��
�����ֱ��y=-
x+1�ڵ�(
��0)��ͬʱ��f��x����g��x�����У�
�ʲ²⺯��f��x����g��x��������Ϊ��y=-
x+1��֤�����£�
�١�f(x)-(-
x+1)=
��
��h(x)=cosx+
x2-x����h��(x)=-sinx+
x-1��
��t(x)=-sinx+
x-1����t��(x)=-cosx+
��0��
��h�䣨x���ڣ�0��+�ޣ��ϵ�����������h�䣨x���ڣ�0��+�ޣ�������ֻ��һ����㣬
��h��(
)=0����h����x���ڣ�0��
���ϵ����ݼ����ڣ�
��+�ޣ��ϵ���������
��h(x)��h(
)=0����f(x)-(-
x+1)��0
��f(x)��-
x+1�ڣ�0��+�ޣ��Ϻ������
�ຯ��f��x����ͼ��λ��ֱ��y=-
x+1���Ϸ���
�ڡ�g(x)-(-
x+1)=sinx-1��0�ڣ�0��+�ޣ��Ϻ������
�ຯ��g��x����ͼ��λ��ֱ��y=-
x+1���·���
�ɴ˿�֪������f��x����g��x�����ڷ����ߣ�y=-
x+1��
��a=
ʱ������f��x����g��x�����ڷ�����Ϊ��y=-
x+1��
| cosx |
| x |
��x=
| �� |
| 2 |
| �� |
| 2 |
������{xn}���Ԧ�Ϊ�����
| �� |
| 2 |
��Sn=
| n�� |
| 2 |
| n(n-1)�� |
| 2 |
| n2�� |
| 2 |
����f��x����g��x����x�ʣ�0��+�ޣ��Ϻ������
��
| cosx |
| x |
| xsinx-cosx |
| x2 |
����(x)=
| xsinx-cosx |
| x2 |
���ա�(x)=
| (xsinx-cosx)��x2-(xsinx-cosx)(x2)�� |
| x4 |
=
| cosx(x2+2) |
| x3 |
��x��0��x2+2��0��
��գ�x��������(0��
| �� |
| 2 |
| �� |
| 2 |
| 3�� |
| 2 |
������(
| �� |
| 2 |
| 3�� |
| 2 |
������(
| 3�� |
| 2 |
| 5�� |
| 2 |
��գ�x���ļ���ֵΪ��(
| �� |
| 2 |
| 1 | ||
|
�ʦգ�x�������ֵΪ��(
| �� |
| 2 |
| 2 |
| �� |
����a��
| 2 |
| �� |
����������f��x����g��x�����ڷ����ߣ����С�f��x����g��x������f��x����g��x����
�ڣ�0��+�ޣ��Ϻ������
��x��0ʱ��f��x��=
| cosx |
| x |
��?x0�ʣ�0��?��ʹ��f��x����g��x������f��x����g��x���ڣ�0��+�ޣ��ϲ��������
��ֻ����f��x����g��x���ڣ�0��+�ޣ��Ϻ������
�ɣ��ã�a��
| 2 |
| �� |
��a=
| 2 |
| �� |
��a=
| 2 |
| �� |
| �� |
| 2 |
��f��(
| �� |
| 2 |
| 2 |
| �� |
| �� |
| 2 |
�����ֱ��y=-
| 2 |
| �� |
| �� |
| 2 |
�ʲ²⺯��f��x����g��x��������Ϊ��y=-
| 2 |
| �� |
�١�f(x)-(-
| 2 |
| �� |
cosx+
| ||
| x |
��h(x)=cosx+
| 2 |
| �� |
| 4 |
| �� |
��t(x)=-sinx+
| 4 |
| �� |
| 4 |
| �� |
��h�䣨x���ڣ�0��+�ޣ��ϵ�����������h�䣨x���ڣ�0��+�ޣ�������ֻ��һ����㣬
��h��(
| �� |
| 2 |
| �� |
| 2 |
| �� |
| 2 |
��h(x)��h(
| �� |
| 2 |
| 2 |
| �� |
��f(x)��-
| 2 |
| �� |
�ຯ��f��x����ͼ��λ��ֱ��y=-
| 2 |
| �� |
�ڡ�g(x)-(-
| 2 |
| �� |
�ຯ��g��x����ͼ��λ��ֱ��y=-
| 2 |
| �� |
�ɴ˿�֪������f��x����g��x�����ڷ����ߣ�y=-
| 2 |
| �� |
��a=
| 2 |
| �� |
| 2 |
| �� |
���������⿼�����Ǻ�����������Ӧ�ã��Ȳ����еȻ���֪ʶ��������������������ȼ�ת��������������ת���������뷽�̡�������������ѧ˼�뷽����

��ϰ��ϵ�д�
�����Ŀ
��ABC����
=
�����������һ���ǣ�������
| a |
| cosB |
| b |
| cosA |
| A�����������ε�����ֱ�������� |
| B��ֱ�������ε����ǵ��������� |
| C������ֱ�������� |
| D�����������λ�ֱ�������� |
���뾶�ֱ�Ϊ2��1����������ȫװ�����߳�Ϊ4���������������У���������ĸ�����Ϊ��������
| A��6 | ||
B��3+2
| ||
C��3+
| ||
D��3+
|
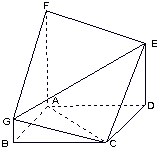 ��ͼ��������ABCDEFG�У�FA��ƽ��ABCD��FA��BG��DE��BG=
��ͼ��������ABCDEFG�У�FA��ƽ��ABCD��FA��BG��DE��BG= ��ͼ��������ABC��AB=3��AC=6����BAC=60�㣬DΪBC�е㣮
��ͼ��������ABC��AB=3��AC=6����BAC=60�㣬DΪBC�е㣮