题目内容
某厂家准备在2014年12月份举行促销活动,依以往的数据分析,经测算,该产品的年销售量x万件(假设该厂生产的产品全部销售),与年促销费用y万元(0≤m≤4)近似满足x=3-
(k为常数),如果不促销,该产品的年销售量只能是1万件,已知2014年生产该产品的固定投入8万元,每生产1万件该产品需要再投入16万元.厂家将每件产品的销售价格规定的每件产品生产平均成本的1.5倍,(产品生产平均成本指固定投入和再投入两部分资金的平均成本).
(1)将2014年该产品的年利润y万元表示为年促销费用m万元的函数;
(2)该厂家2014年的年促销费用投入为多少万元时,该厂家的年利润最大?并求出最大年利润.
| k |
| m+1 |
(1)将2014年该产品的年利润y万元表示为年促销费用m万元的函数;
(2)该厂家2014年的年促销费用投入为多少万元时,该厂家的年利润最大?并求出最大年利润.
考点:函数最值的应用
专题:计算题,应用题,函数的性质及应用
分析:(1)代入m=0,x=1求得k=2,每件新产品的销售价格为1.5×
元,从而求利润y=x•1.5×
-(8+16x+m)并化简;
(2)由基本不等式求最值.
| 8+16x |
| x |
| 8+16x |
| x |
(2)由基本不等式求最值.
解答:
解:(1)由m=0,x=1得,k=2,则x=3-
,
每件新产品的销售价格为:1.5×
(元),
则2014年该产品的年利润y=x•1.5×
-(8+16x+m)
=4+8x-m=4+8(3-
)-m
=-(
+m+1)+29,(0≤m≤4).
(2)∵y=-(
+m+1)+29≤-2
+29=21,
(当且仅当
=m+1,m=3时,等号成立).
即该厂家2014年的年促销费用投入为3万元时,该厂家的年利润最大,最大年利润为21万元.
| 2 |
| m+1 |
每件新产品的销售价格为:1.5×
| 8+16x |
| x |
则2014年该产品的年利润y=x•1.5×
| 8+16x |
| x |
=4+8x-m=4+8(3-
| 2 |
| m+1 |
=-(
| 16 |
| m+1 |
(2)∵y=-(
| 16 |
| m+1 |
| 16 |
(当且仅当
| 16 |
| m+1 |
即该厂家2014年的年促销费用投入为3万元时,该厂家的年利润最大,最大年利润为21万元.
点评:本题考查了学生将实际问题转化为数学问题的能力及基本不等式的应用,属于中档题.

练习册系列答案
相关题目
已知椭圆C1、C2的离心率分别为e1、e2,若椭圆C1比C2更圆,则e1与e2的大小关系正确的是( )
| A、e1<e2 |
| B、e1=e2 |
| C、e1>e2 |
| D、e1、e2大小不确定 |
已知不等式-2xy≤ax2+2y2,若对任意x∈[1,2]及y∈[-1,3]不等式恒成立,则实数a的范围是( )
A、0≤a≤
| ||
| B、a≥0 | ||
C、a≥
| ||
D、a≥-
|
函数f(x)=1-2sinx(sinx+
cosx)的图象向右平移
个单位得函数g(x)的图象,则函数g(x)的解析式是( )
| 3 |
| π |
| 3 |
A、g(x)=2sin(2x-
| ||
| B、g(x)=2cos2x | ||
C、g(x)=2cos(2x+
| ||
D、g(x)=2sin(2x+
|
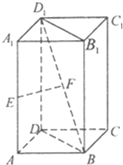 如图,已知棱柱ABCD-A1B1C1D1的底面是正方形,且AA1⊥平面ABCD,E为棱AA1的中点,F为线段BD1的中点.
如图,已知棱柱ABCD-A1B1C1D1的底面是正方形,且AA1⊥平面ABCD,E为棱AA1的中点,F为线段BD1的中点.