题目内容
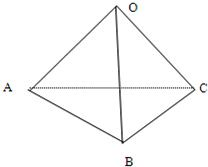 如图所示,已知空间四边形OABC中,OB=|OC|,且∠AOB=∠AOC,则
如图所示,已知空间四边形OABC中,OB=|OC|,且∠AOB=∠AOC,则| OA |
| CB |
| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
考点:异面直线及其所成的角
专题:平面向量及应用
分析:利用OB=OC,以及两个向量的数量积的定义化简cosβ的值,
解答:
解:∵OB=OC,
∴cosβ=
=
=
=
=0;
故选A.
∴cosβ=
| ||||
|
|
| ||||||
|
|
| ||||||||
|
|
=
| ||||||||
|
|
故选A.
点评:本题考查两个向量的数量积的定义,两个向量的夹角公式的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知非零向量
,
满足|
|=3|
|,且关于x的函数f(x)=
x3+
|
|x2+
•
x为R上增函数,则
,
夹角的取值范围是( )
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
| a |
| a |
| b |
| a |
| b |
A、[0,
| ||||
B、[0,
| ||||
C、(
| ||||
D、(
|
下面四个不等式中解集为R的是( )
| A、-x2+x+1≥0 | ||||
B、x2-2
| ||||
| C、2x2-3x+4<0 | ||||
| D、x2+6x+10>0 |
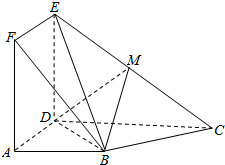 正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=
正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=