题目内容
如果存在非零常数c,对于函数y=f(x)定义域R上的任意x,都有f(x+c)>f(x)成立,那么称函数为“Z函数”.
(1)求证:若y=f(x)(x∈R)是单调函数,则它是“Z函数”;
(2)若函数g(x)=ax3+bx2是“Z函数”,求实数a、b满足的条件.
(1)求证:若y=f(x)(x∈R)是单调函数,则它是“Z函数”;
(2)若函数g(x)=ax3+bx2是“Z函数”,求实数a、b满足的条件.
考点:函数单调性的判断与证明,进行简单的合情推理
专题:证明题,函数的性质及应用
分析:(1)由y=f(x)(x∈R)是单调函数,若是增函数,则当c>0时,函数为“Z函数”;若是减函数,则当c<0时,函数为“Z函数”,从而得证;
(2)由函数g(x)=ax3+bx2是“Z函数”,则函数g(x)满足定义,由g′(x)≥0或g′(x)≤0恒成立,讨论分析可得实数a,b满足的条件是a≠0且b=0.
(2)由函数g(x)=ax3+bx2是“Z函数”,则函数g(x)满足定义,由g′(x)≥0或g′(x)≤0恒成立,讨论分析可得实数a,b满足的条件是a≠0且b=0.
解答:
证明:(1)若y=f(x)(x∈R)是单调函数,
若y=f(x)(x∈R)是增函数,则当c>0时,都有f(x+c)>f(x)成立,函数为“Z函数”.
若y=f(x)(x∈R)是减函数,则当c<0时,都有f(x+c)>f(x)成立,函数为“Z函数”.
(2)若函数g(x)=ax3+bx2是“Z函数”,
则函数g(x)=ax3+bx2是单调函数,即g′(x)可能恒大于0或恒小于等于0,
g′(x)=(ax3+bx2)′=3ax2+2bx,
∴g′(x)=3ax2+2bx≥0或g′(x)=3ax2+2bx≤0恒成立,
∴
或
∴a>0且b=0或a<0,b=0,
由于题目中是存在非零常数c,那么c完全可以取到特别大的实数更大,那么y=3ax2+2bx的单调性由于c过大,完全可以认为是单调增,忽略但调减的区间,所以b∈R
∴实数a、b满足的条件是a≠0.
若y=f(x)(x∈R)是增函数,则当c>0时,都有f(x+c)>f(x)成立,函数为“Z函数”.
若y=f(x)(x∈R)是减函数,则当c<0时,都有f(x+c)>f(x)成立,函数为“Z函数”.
(2)若函数g(x)=ax3+bx2是“Z函数”,
则函数g(x)=ax3+bx2是单调函数,即g′(x)可能恒大于0或恒小于等于0,
g′(x)=(ax3+bx2)′=3ax2+2bx,
∴g′(x)=3ax2+2bx≥0或g′(x)=3ax2+2bx≤0恒成立,
∴
|
|
∴a>0且b=0或a<0,b=0,
由于题目中是存在非零常数c,那么c完全可以取到特别大的实数更大,那么y=3ax2+2bx的单调性由于c过大,完全可以认为是单调增,忽略但调减的区间,所以b∈R
∴实数a、b满足的条件是a≠0.
点评:本题主要考查了函数单调性的判断与证明,考查了进行简单的合情推理的能力,考查了转化思想,属于中档题.

练习册系列答案
相关题目
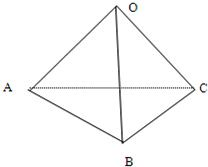 如图所示,已知空间四边形OABC中,OB=|OC|,且∠AOB=∠AOC,则
如图所示,已知空间四边形OABC中,OB=|OC|,且∠AOB=∠AOC,则| OA |
| CB |
| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
在正方体AC1中,下列关系正确的是( )
| A、A1C1⊥AD |
| B、A1C1⊥BD |
| C、D1C1与AB异面 |
| D、AC1∥DC |