题目内容
已知角α的顶点在原点,始边与x轴的正半轴重合,终边经过点P(-3,
),则行列式
的值为 .
| 3 |
|
考点:任意角的三角函数的定义,二阶行列式的定义
专题:三角函数的求值
分析:利用任意角的三角函数的定义,求出sinα,cosα,tanα的值,然后化简行列式求解即可.
解答:
解:角α的顶点在原点,始边与x轴的正半轴重合,终边经过点P(-3,
),
∴OP=
=2
.
∴sinα=
,cosα=-
,tanα=-
.
=sinαcosα-tanα=
×(-
)+
=
.
故答案为:
.
| 3 |
∴OP=
(-3)2+(
|
| 3 |
∴sinα=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
|
| 1 |
| 2 |
| ||
| 2 |
| ||
| 3 |
| ||
| 12 |
故答案为:
| ||
| 12 |
点评:本题考查任意角的三角函数的定义,行列式的定义的应用,基本知识的考查.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
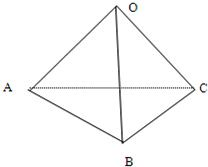 如图所示,已知空间四边形OABC中,OB=|OC|,且∠AOB=∠AOC,则
如图所示,已知空间四边形OABC中,OB=|OC|,且∠AOB=∠AOC,则| OA |
| CB |
| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
 如图所示,在四边形ABCD中,已知A(2,6),B(6,4)、C(5,0)、D(1,0),求直线AC与BD交点P的坐标.
如图所示,在四边形ABCD中,已知A(2,6),B(6,4)、C(5,0)、D(1,0),求直线AC与BD交点P的坐标.