题目内容
13.PA⊥平面ABCD,四边形ABCD是矩形,PA=AD为定长,当AB的长度变化时,异面直线PC与AD所成角的取值范围是($\frac{π}{4}$,$\frac{π}{2}$).分析 以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出异面直线PC与AD所成角的取值范围.
解答 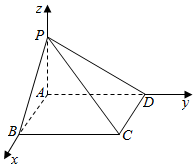 解:以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
解:以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
设PA=AD,AB=x,
则P(0,0,a),C(x,a,0),D(0,a,0),A(0,0,0),
$\overrightarrow{AD}$=(0,a,0),$\overrightarrow{PC}$=(x,a,-a),
设异面直线PC与AD所成角为θ,
则cosθ=$\frac{|\overrightarrow{AD}•\overrightarrow{PC}|}{|\overrightarrow{AD}|•|\overrightarrow{PC}|}$=$\frac{{a}^{2}}{a\sqrt{2{a}^{2}+x}}$,
∵x>0,∴当x→0时,cosθ→$\frac{\sqrt{2}}{2}$,θ→$\frac{π}{4}$;
当x→+∞时,cosθ→0,θ→$\frac{π}{2}$.
∴异面直线PC与AD所成角的取值范围是($\frac{π}{4},\frac{π}{2}$).
故答案为:$(\frac{π}{4},\frac{π}{2})$.
点评 本题考查异面直线所成角的取值范围的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
3.在区间(0,100)上任取一数x,则lg x>1的概率是( )
| A. | 0.1 | B. | 0.5 | C. | 0.8 | D. | 0.9 |
3.有一个容量为60的样本,数据的分组及各组的频数如下:
[11.5,15.5)2;
[15.5,19.5)4;
[19.5,23.5)5;
[23.5,27.5)16;
[27.5,31.5)1l;
[31.5,35.5)12;
[35.5.39.5)7;
[39.5,43.5)3;
根据样本的频率分布估计,数据落在[27.5,39.5)的概率约是( )
[11.5,15.5)2;
[15.5,19.5)4;
[19.5,23.5)5;
[23.5,27.5)16;
[27.5,31.5)1l;
[31.5,35.5)12;
[35.5.39.5)7;
[39.5,43.5)3;
根据样本的频率分布估计,数据落在[27.5,39.5)的概率约是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
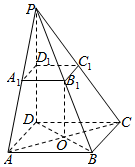 在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.
在四棱锥P-ABCD中,底面ABCD是菱形,PD⊥平面ABCD,点D1为棱PD的中点,过D1作与平面ABCD平行的平面与棱PA,PB,PC相交于A1,B1,C1,∠BAD=60°.