题目内容
18.若{an}的前n项和为Sn,点(n,Sn)均在函数y=$\frac{3}{2}{x^2}-\frac{1}{2}x$的图象上.(1)求数列{an}的通项公式;
(2)设${b_n}=\frac{3}{{{a_n}{a_{n+1}}}}$,Tn是数列{bn}的前n项和,求:使得${T_n}>\frac{m}{20}$对所有n∈N*都成立的最大正整数m.
分析 (1)根据点(n,Sn)均在函数图象上,把点坐标代入确定出Sn,由an=Sn-Sn-1确定出通项公式即可;
(2)根据(1)确定出bn与Tn,根据Tn是增函数,求出Tn的最小值T1,令$\frac{m}{20}$小于最小值,求出最大正整数m的值即可.
解答 解:(1)由题意知:Sn=$\frac{3}{2}$n2-$\frac{1}{2}$n,
当n≥2时,an=Sn-Sn-1=3n-2,
当n=1时,a1=1,适合上式,
则an=3n-2;
(2)根据题意得:bn=$\frac{3}{{a}_{n}{a}_{n+1}}$=$\frac{3}{(3n-2)(3n+1)}$=$\frac{1}{3n-2}$-$\frac{1}{3n+1}$,Tn=b1+b2+…+bn=1-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{7}$+…+$\frac{1}{3n-2}$-$\frac{1}{3n+1}$=1-$\frac{1}{3n+1}$,
∴{Tn}在n∈N*上是增函数,∴(Tn)min=T1=$\frac{3}{4}$,
要使Tn>$\frac{m}{20}$对所有n∈N*都成立,只需$\frac{m}{20}$<$\frac{3}{4}$,即m<15,
则最大的正整数m为14.
点评 此题考查了数列的求和,以及数列递推式,熟练掌握数列的性质是解本题的关键.

练习册系列答案
相关题目
10.在区间〔-3,3〕上随机选取一个数x,则|x|≤1的概率为( )
| A. | $\frac{1}{\begin{array}{l}3\end{array}}$ | B. | $\frac{2}{\begin{array}{l}3\end{array}}$ | C. | $\frac{1}{\begin{array}{l}4\end{array}}$ | D. | $\frac{1}{2}$ |
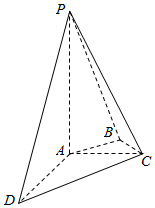 如图,在四棱锥P-ABCD中,PA丄平面ABCD,AC丄AD,AB丄BC,∠BAC=45°,AD=2,AC=1,直线PA与平面PCD所成的角的正弦值为$\frac{{\sqrt{6}}}{6}$.
如图,在四棱锥P-ABCD中,PA丄平面ABCD,AC丄AD,AB丄BC,∠BAC=45°,AD=2,AC=1,直线PA与平面PCD所成的角的正弦值为$\frac{{\sqrt{6}}}{6}$.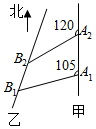 如图,甲船以每小时$30\sqrt{2}$海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里,当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距$10\sqrt{2}$海里,问乙船每小时航行多少海里?
如图,甲船以每小时$30\sqrt{2}$海里的速度向正北方航行,乙船按固定方向匀速直线航行,当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里,当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距$10\sqrt{2}$海里,问乙船每小时航行多少海里?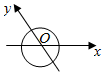 如图,Ox、Oy是平面内相交成120°的两条数轴,${\overrightarrow e_1}$,${\overrightarrow e_2}$分别是与x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x${\overrightarrow e_1}$+y${\overrightarrow e_2}$,则将有序实数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标.若$\overrightarrow{OP}$=(3,2),则|$\overrightarrow{OP}$|=$\sqrt{7}$.
如图,Ox、Oy是平面内相交成120°的两条数轴,${\overrightarrow e_1}$,${\overrightarrow e_2}$分别是与x轴、y轴正方向同向的单位向量,若向量$\overrightarrow{OP}$=x${\overrightarrow e_1}$+y${\overrightarrow e_2}$,则将有序实数对(x,y)叫做向量$\overrightarrow{OP}$在坐标系xOy中的坐标.若$\overrightarrow{OP}$=(3,2),则|$\overrightarrow{OP}$|=$\sqrt{7}$.