题目内容
11.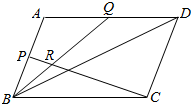 如图所示,?ABCD中,P点在线段AB上,且$\frac{AP}{PB}$=m,Q在线段AD上,且$\frac{AQ}{QD}$=n,BQ与CP相交于点R,求$\frac{PR}{RC}$的值.
如图所示,?ABCD中,P点在线段AB上,且$\frac{AP}{PB}$=m,Q在线段AD上,且$\frac{AQ}{QD}$=n,BQ与CP相交于点R,求$\frac{PR}{RC}$的值.
分析 延长CP,DA交于E点,根据相似三角形的性质,可得$\frac{PR}{RC}$的值.
解答  解:延长CP,DA交于E点,如图所示:
解:延长CP,DA交于E点,如图所示:
则由△PBC∽△PEA得:∴$\frac{AE}{BC}$=$\frac{PE}{PC}$=$\frac{AP}{PB}$=m,
故AE=mBC,PE=mPC,
由$\frac{AQ}{QD}$=n可得:AQ=$\frac{n}{n+1}AD$=$\frac{n}{n+1}BC$,
由△RBC∽△REQ得:$\frac{RE}{RC}$=$\frac{QE}{BC}$=$\frac{AQ+AE}{BC}$=$\frac{\frac{n}{n+1}BC+mBC}{BC}$=$\frac{n}{n+1}+m$,
∴RE=PE+PR=mPC+PR=m(PR+RC)+PR=(m+1)PR+mRC=($\frac{n}{n+1}+m$)RC,
∴(m+1)PR=$\frac{n}{n+1}$RC,
∴$\frac{PR}{RC}$=$\frac{n}{(m+1)(n+1)}$
点评 本题考查的知识点是相似三角形的判定与性质,数形结合思想,难度中档.

练习册系列答案
相关题目
2.若a<0<b,则下列不等式恒成立的是( )
| A. | $\frac{1}{a}>\frac{1}{b}$ | B. | -a>b | C. | a2>b2 | D. | a3<b3 |
6.已知函数f(x)=$\sqrt{3}$sinωx+cosωx(ω>0)的图象与x轴交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列,把函数f(x)的图象沿x轴向右平移$\frac{π}{6}$个单位,得到函数g(x)的图象.若在区间[0,π]上随机取一个数x,则事件“g(x)≥1”发生的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
20.已知a=0.80.7,b=log23,c=log0.32,则a,b,c大小关系是( )
| A. | c<b<a | B. | a<b<c | C. | a<c<b | D. | c<a<b |