题目内容
3.设等比数列{an}的前n项和为Sn,若a1a2a3=64,且${S_{2n}}=5({a_1}+{a_3}+{a_5}+…+{a_{2n-1}})\;\;(n∈{N^*})$,则an=4n-1.分析 利用等比数列的性质结合已知条件求解.
解答 解:∵等比数列{an}的前n项和为Sn,a1a2a3=64,且${S_{2n}}=5({a_1}+{a_3}+{a_5}+…+{a_{2n-1}})\;\;(n∈{N^*})$,
∴利用等比数列的性质可得,a1a2a3=a23=64,即a2=4,
∵S2n=5(a1+a3+…+a2n-1)
∴n=1时有,S2=a1+a2=5a1,
解得a1=1,q=4,
∴an=4n-1.
故答案为:4n-1.
点评 本题考查等比数列的通项公式的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
10.已知函数f(x)=ax-3(a>0且a≠1),f(x0)=0,若x0∈(0,1),则实数a的取值范围是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,+∞) |
14.已知f(x)是定义在R上的奇函数,且当x∈(0,+∞)时,f(x)=log2x,在f(-8)=( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -3 |
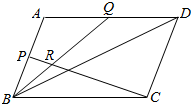 如图所示,?ABCD中,P点在线段AB上,且$\frac{AP}{PB}$=m,Q在线段AD上,且$\frac{AQ}{QD}$=n,BQ与CP相交于点R,求$\frac{PR}{RC}$的值.
如图所示,?ABCD中,P点在线段AB上,且$\frac{AP}{PB}$=m,Q在线段AD上,且$\frac{AQ}{QD}$=n,BQ与CP相交于点R,求$\frac{PR}{RC}$的值.