题目内容
18.满足z+$\frac{5}{z}$是实数且z+3的实数与虚部是相反数的虚数z是否存在?若存在,求出虚数z,若不存在,请说明理由.分析 利用复数的定义和性质列出方程组能求出z.
解答 解:虚数z存在.
设z=a+bi,
∵满足z+$\frac{5}{z}$是实数且z+3的实部与虚部是相反数,
∴$\left\{\begin{array}{l}{a+bi+\frac{5}{a+bi}=(a+bi)+\frac{5(a-bi)}{{{a}^{2}+{b}^{2}}_{\;}}∈R}\\{a+3=-b}\end{array}\right.$,
解得得 a=-1,b=-2或a=-2,b=-1.
∴z=-1-2i或z=-2-i.
点评 本题考查满足条件的复数的求法,是基础题,解题时要认真审题,注意复数的性质的合理运用.

练习册系列答案
相关题目
9.已知抛物线y2=4x的过焦点的弦AB被焦点分成长为d1、d2的两段,那么( )
| A. | d1+d2=d1•d2 | B. | d1-d2=d1•d2 | C. | d12+d22=d1•d2 | D. | d12-d22=d1•d2 |
10.已知函数f(x)=ax-3(a>0且a≠1),f(x0)=0,若x0∈(0,1),则实数a的取值范围是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,+∞) |
10.阅读如图所示的程序框图,若输入a=$\frac{9}{19}$,则输出的k值是( )
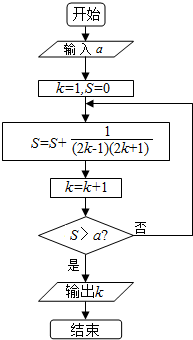

| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
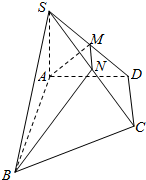 如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,CD=DA=a,AB=2a,SA⊥平面ABCD,且SA=a
如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,CD=DA=a,AB=2a,SA⊥平面ABCD,且SA=a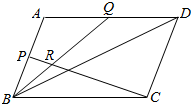 如图所示,?ABCD中,P点在线段AB上,且$\frac{AP}{PB}$=m,Q在线段AD上,且$\frac{AQ}{QD}$=n,BQ与CP相交于点R,求$\frac{PR}{RC}$的值.
如图所示,?ABCD中,P点在线段AB上,且$\frac{AP}{PB}$=m,Q在线段AD上,且$\frac{AQ}{QD}$=n,BQ与CP相交于点R,求$\frac{PR}{RC}$的值.