题目内容
3.若f(x)=x3-x${\;}^{\frac{1}{2}}$,则满足f(x)<0的x的取值范围是(0,1).分析 先由题意化简不等式,在同一个坐标系中画出y=x3和y=$\sqrt{x}$的图象,由图象求出不等式的解集.
解答 解:由题意得,f(x)<0为x3-$\sqrt{x}$<0,
则x3<$\sqrt{x}$,且x≥0,
在同一个坐标系中画出y=x3和y=$\sqrt{x}$的图象:
由图得,不等式x3<$\sqrt{x}$的解集是(0,1),
故答案为:(0,1).
点评 本题考查利用幂函数的图象求不等式的解集,考查数形结合思想,属于基础题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
20.如图程序框图,输出a的结果为( )


| A. | 初始值a | B. | 三个数中的最大值 | ||
| C. | 三个数中的最小值 | D. | 初始值c |
1.设集合U=R,A={x|(x+l) (x-2)<0},则∁UA=( )
| A. | (一∞,-1)∪(2,+∞) | B. | [-l,2] | C. | (一∞,-1]∪[2,+∞) | D. | (一1,2) |
18.设集合I={3,4,5,6,7,8,9},A={8,9},则满足B⊆I,且A∩B≠∅中的集合B的个数为( )
| A. | 160 | B. | 96 | C. | 64 | D. | 128 |
8.已知所数f(x)=2cosωx-2sinωx(ω>0)在(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递减,则当ω取得最大值时,下列说法正确的是( )
| A. | ω=2 | B. | 函数f(x)的对称轴为x=-$\frac{π}{2}$+kx(k∈Z) | ||
| C. | 函数f(x)的对称中心为($\frac{π}{2}$+kx,0)(k∈Z) | D. | 函数f(x)在[$\frac{π}{2}$,$\frac{2π}{3}$]上的最小值为-$\sqrt{3}$+1 |
15.一个口袋中装有2个白球和3个黑球,这5个球除颜色外完全相同,从中摸出2个球,则这2个球颜色相同的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
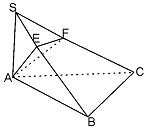 如图所示,SA⊥平面ABC,AB⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F.
如图所示,SA⊥平面ABC,AB⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F.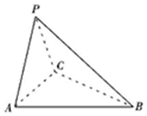 如图,三棱锥P-ABC中,PA=PC,底面ABC为正三角形.
如图,三棱锥P-ABC中,PA=PC,底面ABC为正三角形.