题目内容
8.已知所数f(x)=2cosωx-2sinωx(ω>0)在(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递减,则当ω取得最大值时,下列说法正确的是( )| A. | ω=2 | B. | 函数f(x)的对称轴为x=-$\frac{π}{2}$+kx(k∈Z) | ||
| C. | 函数f(x)的对称中心为($\frac{π}{2}$+kx,0)(k∈Z) | D. | 函数f(x)在[$\frac{π}{2}$,$\frac{2π}{3}$]上的最小值为-$\sqrt{3}$+1 |
分析 化函数f(x)为余弦型函数,利用余弦函数的单调性求得f(x)的减区间,结合条件可求得ω的最大值,再写出f(x)的解析式,从而判断选项是否正确即可.
解答 解:函数f(x)=2cosωx-2sinωx=2$\sqrt{2}$cos(ωx+$\frac{π}{4}$)(ω>0)在(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递减,
∴2kπ≤ωx+$\frac{π}{4}$≤2kπ+π,求得-$\frac{π}{4ω}$+$\frac{2kπ}{ω}$≤x≤$\frac{3π}{4ω}$+$\frac{2kπ}{ω}$ (k∈Z).
∵f(x)在(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递减,
∴-$\frac{π}{4ω}$≤-$\frac{π}{2}$,且$\frac{3π}{4ω}$≥$\frac{π}{2}$,
求得 0<ω≤$\frac{1}{2}$,∴ωmax=$\frac{1}{2}$,A错误;
∴f(x)=2$\sqrt{2}$cos($\frac{1}{2}$x+$\frac{π}{4}$),
令$\frac{1}{2}$x+$\frac{π}{4}$=kπ,k∈Z,解得f(x)的对称轴是x=2kπ-$\frac{π}{2}$,k∈Z,B错误;
令$\frac{1}{2}$x+$\frac{π}{4}$=kπ+$\frac{π}{2}$,k∈Z,解得f(x)的对称中心是(2kπ+$\frac{π}{2}$,0),k∈Z,C错误;
x∈[$\frac{π}{2}$,$\frac{2π}{3}$]时,$\frac{1}{2}$x+$\frac{π}{4}$∈[$\frac{π}{2}$,$\frac{7π}{12}$],f(x)是单调减函数,
其最小值为2$\sqrt{2}$cos$\frac{7π}{12}$=-$\sqrt{3}$+1,D正确.
故选:D.
点评 本题主要考查两角和的余弦公式以及余弦函数的单调性问题,是综合题.

| A. | 4 | B. | 1 | C. | 18 | D. | $\frac{4}{5}$ |
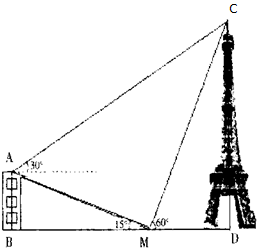 如图,一栋建筑物AB高(30-10$\sqrt{3}$)m,在该建筑 物的正东方向有一个通信塔CD.在它们之间的地面M点(B、M、D三点共线)测得对楼顶A、塔顶C的仰角分别是15°和60°,在楼顶A处 测得对塔顶C的仰角为30°,则通信塔CD的高为60m.
如图,一栋建筑物AB高(30-10$\sqrt{3}$)m,在该建筑 物的正东方向有一个通信塔CD.在它们之间的地面M点(B、M、D三点共线)测得对楼顶A、塔顶C的仰角分别是15°和60°,在楼顶A处 测得对塔顶C的仰角为30°,则通信塔CD的高为60m.