题目内容
12.在△ABC中,a,b,c分别是角A,B,C的对边,且b,c是关于x的一元二次方程x2+mx-a2+b2+c2=0的两根.(1)求角A的大小;
(2)已知a=$\sqrt{3}$,设B=θ,△ABC的面积为y,求y=f(θ)的最大值.
分析 (1)由已知化简可得:b2+c2=a2+bc,利用余弦定理可求cosA=$\frac{1}{2}$,结合范围A∈(0,π),可求A的值.
(2)由已知及正弦定理可得b=2sinθ,c=2sin($\frac{2π}{3}$-θ),利用,三角形面积公式,三角函数恒等变换的应用化简可求y=$\frac{\sqrt{3}}{2}$sin(2θ-$\frac{π}{6}$)+$\frac{\sqrt{3}}{4}$,由0<θ<$\frac{2π}{3}$,可得范围-$\frac{π}{6}$<2θ-$\frac{π}{6}$<$\frac{7π}{6}$,利用正弦函数的图象可求最大值.
解答 (本题满分为12分)
解:(1)在△ABC中,由题意可得:bc=-a2+b2+c2,可得:b2+c2=a2+bc,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{1}{2}$,
又∵A∈(0,π),
∴A=$\frac{π}{3}$.…6分
(2)由a=$\sqrt{3}$,A=$\frac{π}{3}$及正弦定理可得:$\frac{b}{sinB}=\frac{c}{sinC}=\frac{a}{sinA}=2$,
∴b=2sinB=2sinθ,c=2sinC=2sin($\frac{2π}{3}$-B)=2sin($\frac{2π}{3}$-θ),
∴y=$\frac{1}{2}$bcsinA=$\sqrt{3}$sinθsin($\frac{2π}{3}$-θ)=$\sqrt{3}$sinθ($\frac{\sqrt{3}}{2}$cosθ+$\frac{1}{2}$sinθ)=$\frac{3}{4}$sin2θ-$\frac{\sqrt{3}}{4}$cos2θ+$\frac{\sqrt{3}}{4}$=$\frac{\sqrt{3}}{2}$sin(2θ-$\frac{π}{6}$)+$\frac{\sqrt{3}}{4}$,
由于0<θ<$\frac{2π}{3}$,可得:-$\frac{π}{6}$<2θ-$\frac{π}{6}$<$\frac{7π}{6}$,
∴当2θ-$\frac{π}{6}$=$\frac{π}{2}$,即θ=$\frac{π}{3}$时,ymax=$\frac{3\sqrt{3}}{4}$.…12分
点评 本题主要考查了余弦定理,正弦定理,三角形面积公式,三角函数恒等变换的应用,正弦函数的图象和性质在解三角形中的应用,考查了转化思想和数形结合思想的应用,属于中档题.

| A. | $\frac{1}{128}$ | B. | $\frac{3}{256}$ | C. | $\frac{1}{64}$ | D. | $\frac{1}{12}$ |
| A. | 3x+4y-12=0或4x-3y+9=0 | B. | 3x+4y-12=0或x=0 | ||
| C. | 4x-3y+9=0或x=0 | D. | 3x-4y+12=0或4x+3y+9=0 |
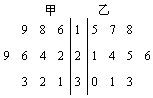 甲、乙两人在10天中每天加工零件的个数用茎叶图表示如图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数.则这十天甲、乙两人每人每日加工零件的平均数的和为49.
甲、乙两人在10天中每天加工零件的个数用茎叶图表示如图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数.则这十天甲、乙两人每人每日加工零件的平均数的和为49.