题目内容
13.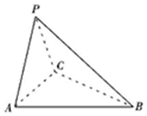 如图,三棱锥P-ABC中,PA=PC,底面ABC为正三角形.
如图,三棱锥P-ABC中,PA=PC,底面ABC为正三角形.(Ⅰ)证明:AC⊥PB;
(Ⅱ)若平面PAC⊥平面ABC,AB=2,PA⊥PC,求三棱锥P-ABC的体积.
分析 (Ⅰ)取AC中点O,连接PO,BO,由等腰三角形的性质可得PO⊥AC,BO⊥AC,再由线面垂直的判定可得AC⊥平面POB,则AC⊥PB;
(Ⅱ)由面面垂直的性质可得PO⊥平面ABC,再由已知求出三角形ABC的面积,即PO的长度,代入棱锥体积公式求得三棱锥P-ABC的体积.
解答 (Ⅰ)证明:如图,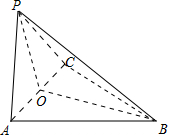
取AC中点O,连接PO,BO,
∵PA=PC,∴PO⊥AC,
又∵底面ABC为正三角形,∴BO⊥AC,
∵PO∩OB=O,∴AC⊥平面POB,则AC⊥PB;
(Ⅱ)解:∵平面PAC⊥平面ABC,且平面PAC∩平面ABC=AC,
PO⊥AC,∴PO⊥平面ABC,
又AB=2,PA⊥PC,可得PO=1,且${S}_{△ABC}=\frac{1}{2}×2×\sqrt{3}=\sqrt{3}$.
∴${V}_{P-ABC}=\frac{1}{3}×\sqrt{3}×1=\frac{\sqrt{3}}{3}$.
点评 本题考查线面垂直的判定,考查空间想象能力和思维能力,训练了多面体体积的求法,是中档题.

练习册系列答案
相关题目
1.设圆x2+y2-2x-2y-2=0的圆心为C,直线l过(0,3)与圆C交于A,B两点,若$|{AB}|=2\sqrt{3}$,则直线l的方程为( )
| A. | 3x+4y-12=0或4x-3y+9=0 | B. | 3x+4y-12=0或x=0 | ||
| C. | 4x-3y+9=0或x=0 | D. | 3x-4y+12=0或4x+3y+9=0 |
8.已知双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{27}$=1的左、右焦点分别为F1、F2,且F2为抛物线y2=2px的焦点,设P为两曲线的一个公共点,则△PF1F2的面积为( )
| A. | 18 | B. | 18$\sqrt{3}$ | C. | 36 | D. | 36$\sqrt{6}$ |
18.已知$\left\{\begin{array}{l}x+2y≥2\\ 3x-y-6≤0\\ 2x-3y+3≥0\end{array}\right.$,且z=x2+y2,则z的最小值是( )
| A. | 4 | B. | 1 | C. | 18 | D. | $\frac{4}{5}$ |
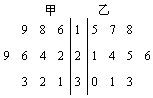 甲、乙两人在10天中每天加工零件的个数用茎叶图表示如图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数.则这十天甲、乙两人每人每日加工零件的平均数的和为49.
甲、乙两人在10天中每天加工零件的个数用茎叶图表示如图,中间一列的数字表示零件个数的十位数,两边的数字表示零件个数的个位数.则这十天甲、乙两人每人每日加工零件的平均数的和为49.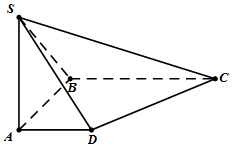 已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$.
已知四棱锥S-ABCD中,四边形ABCD是直角梯形,∠ABC=∠BAD=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$.